---

It is important to extend the normal mode procedure to variable sound speed profiles. The strategy here is a new one, based on representing the solution in terms of spanning functions from an iso-velocity solution that is in some average sense close to the variable profile and making use of elements of Sturm-Louiville theory. The following method was developed after an unsuccessful attempt to include a variable sound speed profile as a perturbation of the iso-velocity case via the usual perturbation theory from elementary quantum mechanics. The first order perturbation is doomed to failure because the lowest modes are relatively small even compared to the smallest perturbation, which makes it impossible to reconstruct the eigenfunctions. It is a well-known fact that the standard perturbation method did not treat perturbed wave functions correctly in terms of the expansion coefficients even though the theory often gave reasonable results for perturbed eigenvalues. Any attempt to add second order terms in a poorly converging first order theory will never work, since, with the exception of forbidden first order processes such as occur in quantum mechanics and result in Fermi’s “first golden rule”, second order corrections are always refinements to the first order calculations at best. The new method excludes any truncation in space or any limiting of parameters in some asymptotic sense; rather it retains the complete space throughout the calculation. Thus, in a sense it is not a perturbation method, but a transformation method, which may be viewed as a new type of matrix - a warping matrix - transforming an iso-velocity space to a variable velocity space. Superficially, the method resembles a Galerkin formulation which has its origin in a completely different philosophy, namely in demanding that any subset of a complete set used to expand an exact solution must be orthogonal to those states not included in the expansion - the residuals. The Galerkin method is one of the weighted residual methods and had its origin in polynomial fitting methods. The Galerkin method is easily subject to error due to the arbitrary nature of basis states and the difficulty of dealing with nested boundary conditions.

The Generalized Eigenvalue Formulation

At this point we examine two ocean models with the same bottom properties. One model has an iso-velocity water column while the other has a variable velocity profile. The bottom properties are the same and are as described above. The solution for the depth-separated wave equation for the iso-velocity case in the water column has been developed above and is expressed now as:

. (1)

The equation that governs the solution for the mode U_m in the water column for arbitrary sound speed profile is:

. (2)

The terms in Eq. (2) can be rearranged in such a way that the left-hand side of the equation contains the operator for the iso-velocity solution:

, (3)

where , and

Recall that for Sturm-Louiville problems we have the orthogonality condition:

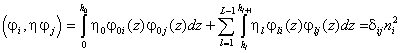(4)

for any two function and . We can assume completeness of the space, namely that the eigenfunctions of the iso-velocity space span the variable velocity space. Then, in particular, within the water column we can decompose the solution for the variable velocity space as:

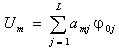. (5)

It is to be understood that for solutions other than in the water column, the functional form is the same, so that for the layers only the normalization and the values of the eigenvalues need to be adjusted for the ’s defined in terms of the ’s. Substituting (5) in the differential Eq. (3), we obtain:

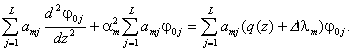
Then using Eq. (1), we arrive at:

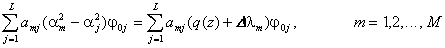. (6)

Multiplying both sides of Eq. (6) by and integrating over only the water column, we obtain:

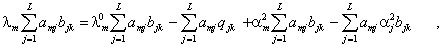(7)

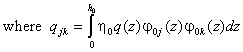and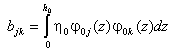, which can be calculated as soon as we have solved the iso-velocity problem, so at this stage they are known. The set of equations (7) can be written in matrix form as follows:

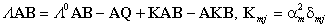. (8)

Keep in mind that matrices Q and B are both symmetric. Here , ⁰, and K are diagonal matrices of the respective eigenvalues, where the diagonal term for row m is the eigenvalue etc.

Matrix Eq. (8) relates the variable velocity eigenvalues with the iso-velocity eigenvalue and the vertical iso-velocity eigenvalues . Here k₀ is the wave number for the iso-velocity (spanning) space, and and are the iso-velocity modal eigenangles and the variable velocity modal eigenangles, respectively. Although the modal angle for the iso-velocity case corresponds to the angle of the mode phase intensity, the angle for the variable velocity is not physical in the same sense, due to refraction - the paths of intensity bend contrary to what a fixed angle would imply. Further, it is somewhat arbitrary since it depends on the iso-velocity wave number. However, the overall eigenvalue should be and is an invariant with respect to the iso-velocity wave number proved the number is within reasonable bounds. We discuss those bounds below but it is suitable to choose the reference wave number corresponding to a sound speed bracketed by the values in the water column. However, the angles do have meaning in the time domain in connection with energy fronts since they are averaged over a large number of frequencies.

Eq. (8) is actually a generalized eigenvalue problem which may be reduced to the following form by using the fact that :

. (9)

Here I is the identity (unit) matrix and k₀ is a scalar. Eq. (9) may be solved by post multiplying both sides by the inverse of B to arrive at a matrix which is not generally symmetric. We then may make use of the QR-algorithm for general non-symmetric or non-Hermitian matrices, which gives us both the eigenvalues and the eigenfunctions at somewhat more computational cost than if we had a symmetric matrix. Because we are essentially dealing with a Sturm-Louiville problem (or a pseudo- Sturm-Louiville problem if we require the continuum), we know that we can transform the problem to one of symmetric form which is computationally desirable and mathematically more aesthetic.

Numerical Algorithm for the Solution of the Generalized Eigenvalue Problem

The first observation which we can make on the approach to solving Eq. (9) by an optimal numerical procedure is that the matrix B is close to the unit matrix since its elements are the inner products of the elements of the major part of the normalized vertical wave functions. Only that part of the wave function that penetrates the sediment is left out, and that component is usually small. Indeed, for a strongly ducted problem with the duct away from the bottom of the water column there exists a subset of B that is essentially a unit matrix. However, B is not only symmetric but positive definite since any part of the norm will be positive. Thus we may employ the most efficient method for LU-decomposition due to Cholesky to decompose B into lower and upper triangular matrices, namely B=L, where is the transpose of the lower triangular matrix L and is, thus, upper triangular. The diagonal elements under the Cholesky scheme are the square roots of the elements of D, the pivot matrix, in standard LDU-decomposition. The scheme requires that both L and its transpose have the same diagonal elements. The next discussion illustrates how simply and efficiently Cholesky decomposition can work for our eigenvalue problem. Here it should be remembered that B is both symmetric and positive definite. We have that:

.

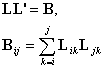This decomposition involves about N³/6 floating point operations (FPO), where N is the size of the matrix, and is probably the fastest known factorization method for a dense matrix. One FPO consists of one floating point multiplication and one addition (operational count).

Following decomposition of B, we post multiply both sides of Eq. (9) by and use the fact that to obtain:

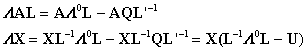, (10)

which now involves a symmetric matrix U= and a new matrix X=AL that is related to the variable velocity case modal functions of Eq. (5). We may efficiently obtain U by solving for the two expressions:

Q=LY (11)

and

. (12)

Since both Q and U are symmetric, we need only find the lower triangular elements of Y from Eq. (11) and the lower triangular elements of U from Eq. (12) to obtain all of the elements of U. Each of these involve N(N+1)/2 FPO’s and are extremely simple to program and very stable.

It remains to determine . To determine this quantity, we first find:

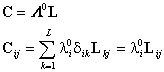. (13)

We note that C is lower triangular since is lower triangular, which means that . Then we determine:

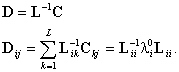(14)

This result follows from the fact that and C are lower triangular, which means that and ; thus k=i=j. Now we need only to determine the diagonal elements of the inverse of , which may be carried out in a manner similar to the above proof and leads to:

.

Thus we have arrived at:

. (15)

This leads to the following equation which replaces Eq. (10):

. (16)

Eq. (16) can be viewed as a generalized eigenvalue problem. In the formulation of our variable velocity profile problem, we may refer to the matrix W as a warping matrix that transforms the iso-velocity eigenfunctions and eigenvalues into the variable velocity space. We may now take advantage of the fact that W is symmetric and transform W to a tridiagonal matrix. This may be performed by either a Givens transformation or a sequence of Householder transformations. A Givens transformation is related to a rotation in two dimensions while the more efficient Householder transformation is related to “inflection” in two dimensions. Both have the effect of leading to a tridiagonal form but the Householder method is about twice as efficient for dense matrices. There are many other advantages to the Householder transformation. First, the Householder matrix is symmetric, unitary, Hermitian and “idempotent” (M*M=M). The Householder transformation for a general symmetric matrix requires only 2N³/3 operations for large values of N. It performs the same procedure as the Gram-Schmidt orthogonalization method but is also much more stable than that procedure, and even more stable than the modified Gram-Schmidt method which sometimes fails to maintain true orthogonality. The product of Householder transformations that leads to a tridiagonal form is a similarity transformation, and thus eigenvalues of the tridiagonal matrix are the same as the original matrix. We then employ the QL-algorithm, which for a tridiagonal symmetric matrix requires on the order of or less than 2N iterations, to obtain the eigenvalues for the variable velocity space. Typically the average number of iterations is fewer than 2N. In the process if we save the sequence of unitary transformations that transforms the matrix W to tridiagonal form, which is easy to do using the Householder method, it is possible to construct the original eigenvectors in a straightforward manner, namely X=AL, which only requires an additional 2N³/3 FPO’s. The procedure is also very stable. Since W may be viewed as being obtained from a similarity transformation of , it has the same eigenvalues as the original problem, namely those associated with A.

Once we obtain X, we may easily obtain A from X=AL with N(N+1) FPO’s. The matrix A has rows that correspond to the expansion coefficients we require for expression (3.31). The complete process is on the order of (3N³/2)+N(1.5N+2) FPO’s.

The method presented here should not be confused with the Galerkin method for finding eigenvalues and eigenfunctions for variable sound speed profiles published earlier in the literature (for example, see [14]). This formulation is based on a completely different theoretical strategy. Appendix 3B contains some comments on the comparison of the two methods, because this question was raised by the audience several times after we had given talks on our technique.

Some Additional Comments on the Numerical Procedure for Determining the Expansion Coefficients

To determine the expansion coefficients a_ij, i.e., the matrix A, we revert to the independent system of equations defined by the warping transformation (16). For weakly ducted profiles we may perform one or two passes of the Gauss-Seidel iterative scheme. However, it is generally not safe to apply this procedure, mainly because some diagonal terms may be rather small even compared to adjacent off-diagonal terms. Since the warping matrix is symmetric and should be positive definite, Cholesky decomposition is a fast approach to solve the system, but we have found some pathologies in that procedure. Thus, it seems the safest method is to use LU-decomposition with pivoting. Note that the diagonal matrix elements are usually dominant. However, it is possible that some diagonal elements are very small, because adjacent eigenvalues of the unperturbed system may be very close to the perturbed case. In such situations it is safe simply to exclude the associated row and column and set the associated coefficient to zero. This amounts to the assumption that that row is not linearly independent. This sort of procedure is frequently done when using the method of singular value decomposition and is associated with a poor condition number or ill-posed problems. There is another reason for doing this. It prevents the possible reversal of parity of the associated eigenfunctions. There is no loss in accuracy and in some sense it may be associated with a type of degeneracy. We find that for very large numbers of modes corresponding to high frequencies, the warping matrix is effectively banded in the sense that most of the elements are negligible due to the rapid fall-off of the 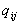’s for [i-j] large. Thus, we may employ banded matrix solvers as we go up in frequency, which greatly increases the speed of solution. Also iterative methods become competitive for high frequency banded matrices. The band effect with increased frequency is an asset, which keeps our method competitive in speed when many normal mode methods become very slow for high frequencies. However, at no point have we noticed instabilities with this method even while retaining rows with small diagonal terms. Deleting rows with relatively small diagonal terms merely guarantees that we retain a positive definite matrix which then allows us to employ the faster Cholesky decomposition and at high frequencies allows us to employ semi-direct iterative methods, such as the conjugate gradient method, which may have an advantage in speed for pronounced bandedness when the number of modes becomes large. Another strategy is to separate the matrix into two blocks, namely, the part that has diagonally dominant terms and the remaining part that does not. We may iterate via the Jacobi method or the Gauss-Seidel method down to the submatrix that does not have diagonally dominant terms. At that point we may use a direct solver for the sub-matrix. We may then iterate one or more times if needed. These strategies and others are presently under investigation since the solver part of the code is the most time intensive at higher frequencies and we should take advantage of high frequency asymptotics.

Calculation of the Matrix Q

Building the matrix elements of Q may be the time consuming operation, so special attention must be paid to performing this operation in an efficient manner. We avoid numerical quadrature as that would be too costly, particularly as one increases the frequency. Therefore an effort has been made to obtain a closed form representation of the matrix elements. We may do this in one of two ways. Recall that

. (17)

We may approximate over any suitably small segment, so we may always express Eq. (17) in that form. This is the so-called pseudo-linear sound speed variation. This allows us to obtain the elements of the matrix Q in closed form.

A more elegant and precise way that generally leads to a faster calculation is the following. Any analytical function can be decomposed in a truncated series of Legendre polynomials:

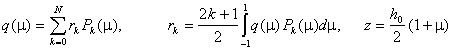, (18)

where the ’s are Legendre polynomials of order j. Gauss-Legendre quadrature requires about twice the number of terms as the highest order of the Legendre polynomial (almost never more than about 10) and are thus quite simple to do. We will not need many expansion terms since q(z) does not have a complicated structure. Typically we may need from 2 to 5 terms. This expansion also smoothes the profile, which is desirable. Regardless of what one measures, nature is never so abrupt.

We now make the transformation of the remainder of the integrand for involving the eigenfunctions of the iso-velocity case:

. (19)

We may rewrite the cosine functions taking into account a change of variables for :

.

We note that :

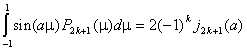
and (20)

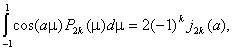
where is a spherical Bessel function of order 2k. Thus, we can express the elements of matrix , in a convenient analytical form:

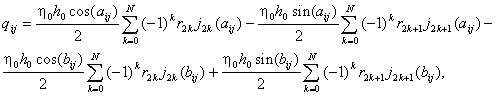(21)

where , . Here the number of terms reduces by a factor of 2 in comparison with the total number of Legendre expansion terms (almost never more than 5) because only even functions give non-zero integrals. The diagonal terms are a special case and much easier to construct. It is noted that Q is symmetric in the indices so we only need to construct half of the off-diagonal elements. We can also save much computer time by noting that [51]:

, (22)

where and are 3-j coefficients from quantum mechanics. We need only make 2L rather than L² sets of spherical Bessel functions, where L is the number of perfectly trapped modes for the iso-velocity case. Whenever possible, we may also make a similar transformation for the sine and cosine functions and store them for multiple use. Thus, rather than L² , we need to construct only 2L sine and cosine functions. Since these functions are fast and easy to make, we have a fast closed form solution of the integrals that define the matrix Q. For high frequency the ’s fall off as they move off the matrix diagonal at a rate such that we do not need to calculate all of the values, and we may set values to zero and invoke bandedness at no loss of accuracy in suitable cases. Clearly, the sine of a large argument varies rapidly, so when indices of q differ much, the integrals approach small numbers relative to the diagonal terms. Indeed, bandedness is more a characteristic of higher frequencies than of lower.

These comments end the part describing the solution of the depth-separated wave-equation for an arbitrary sound speed profile. It is important to note that one of the advantages of the normal mode approach is that vertical modal functions do not depend on the receiver-source geometry. Once calculated, they can be stored and used many times if the ocean environment investigated is the same.