---

The normal mode method is usually the fastest approach for range independent environments with the exception of low frequencies and/or for ocean bottoms in which elastic properties are important. In that case the wave integration technique, namely the FFP-program, is very useful since it is accurate for near field effects and is more easily implemented for elastic bottoms. Both the NM and FFP methods are based on the technique of separation of variables and can be used to predict the acoustic field at any point without marching out from a source, as is required in marching PE methods. Recently PE models have been the most used models to predict the propagation of sound in an ocean channel that varies in range. In principle, any PE derivation arrives at a one-way wave equation (negligible incoming field means weak backscattering effects), with the second derivative in range eliminated on physical grounds. Thus, one gains computational speed since the solution in range involves a one-way marching algorithm. The initial SPE by Hardin and Tappert involved limitations in the angle interval of the propagation for sound with respect to the main propagation direction - the interval was assumed to be small. However, recent developments have enabled researchers to expand the allowable range of angular propagation practically up to ninety degrees. M. Collins has in particular expanded the applicability of the PE by increasing the allowed angle of propagation and by allowing for more complicated, even elastic ocean bottoms. These more complicated PE models require many initial parameters, such as the number of Padè approximation terms, a depth of the false soft bottom, parameters for the artificial absorption layer, the vertical sampling interval, the marching step-size in range, etc., which do not have a solid physical basis for their choice. The dependence of the solution stability on the set of parameters has not been investigated in detail. The particular choice of parameters influences the final result, so it gets very complicated to interpret the physics of the phenomenon from the modeling results, especially if one deals with pulse propagation in an ocean channel. No finite-element or finite-difference methods, which are usually implemented in known normal mode models such as KRAKEN, and have very frequency-dependent vertical and horizontal mesh sizes, can compete in computational time with the most recent PE models. Thus, it has been very challenging for us to create a competitive (in time) range-dependent propagation model based on the normal mode approach, which would deal with range dependence on an optimal basis using the fact that the NM approach is the fastest one for range-independent parts of the propagation path. Further, the use of modes which have physical relevance yields valuable information in understanding many physical features of a particular phenomenon, not the least of which is understanding the processes responsible for the arrival times of pulses. With the advent of the computational methods and incorporated in the computer code SWAMP, which contains closed analytical forms of the vertical modal functions, it is easy to compute mode coupling coefficients between two range-independent regions - usually the most time consuming part of mode coupling methods. This very favorable fact along with the speed and versatility of the range-independent part of the algorithm can make the model very competitive with PE models.

Even though NM methods are inherently range independent, they can be used as a range-dependent tool by dividing the range into sub-regions that have range-independent characteristics and then coupling the modal solutions from region to region by suitable interface conditions. It should be remembered that the wave equation requires both pressure and particle velocity conservation, so that if one wishes to obtain the full wave solution, one must impose both boundary conditions. Evans developed an important solution of this problem by coupling both backward and forward going solutions. Following his derivation, we can divide the axisymmetric range-dependent ocean channel into N segments in range, as shown in Fig. 3.2, within which all the ocean parameters are approximately range-independent. Clearly, just as finite range methods divide solutions into discrete parts in which the parameters are fixed (constant in a region), a coupled modal solution need not be any more limiting in accuracy than the PE one, and indeed can lead to more accuracy, since it can deal with the two-way solution and never drop the second order differential terms as a requirement. The general solution of the Helmholtz equation for the j-th subregion, which is far enough from the source so that only discrete modes contribute, is:

, (1)

where the solution is written for the pressure variable to follow Evans’ derivation and is a solution for subregion j. represent the scaled Hankel functions of the first kind (outgoing or emitted wave) and second kind (incoming or backscattered wave):

(2)

(3)

where is the modal horizontal wavenumber, and in the special case when j=1. The scaling is done to avoid numerical overflow problems involving growing and decaying exponentials. It is more convenient to replace the Hankel functions by their large-argument asymptotic representation:

(4)

(5)

The coefficients and of Eq. (1) can be found from the interface boundary conditions. First, we impose continuity of pressure at the j-th interface:

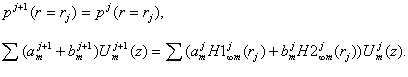(6)

Applying the orthogonality conditions for the modal functions from subregion (j+1), , we arrive at the following expression:

(7)

where the integral is taken over the whole vertical space from the surface to the terminating bottom depth. Equation (7) can be written in matrix-vector form as:

, (8)

where are diagonal matrices and , are column vectors.

To get enough equations to determine both sets of the coefficients and , we have to impose the second interface conditions -- continuity of radial particle velocity. The radial particle velocity can be calculated as:

(9)

where terms were neglected in the final sum because of being next order smallness terms for the far field approximation. Applying the same orthogonality conditions as for obtaining Eq. (7), we have:

. (10)

In matrix notation, it is

. (11)

Combining Eq. (11) with Eq. (8), we can obtain an explicit iterative expression:

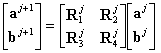, (12)

where

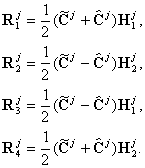(13)

To close the iterative procedure, we need to include the boundary conditions at r=0 and radiation conditions as . The radiation condition requires a zero backscattering field which means The appropriate condition at r=0 can be derived as a NM solution of a range-independent environment with a point source at z= :

. (14)

Collecting all of these equations together, we obtain a block matrix problem of the following form:

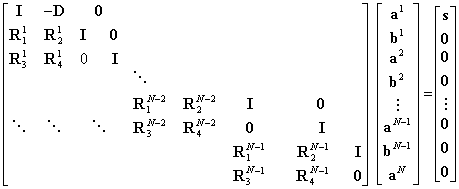, (15)

where D is a diagonal matrix with elements

, (16)

and s is a column vector with elements:

. (17)

Unfortunately, since all solutions in a two-way wave equation are connected, the two-way coupled mode problem (15) requires global solution of a whole family of normal-mode problems, one for each segment, followed by the solution of a large banded, block-linear system. Thus, this general approach by Evans leads to a slow and cumbersome numerical algorithm. Researchers have dealt with the one-way coupled mode solution with some success, since one way mode coupling should in no way be more limiting than any PE method. An efficient marching implementation of coupled modes can be done in several ways with different degrees of accuracy. The problem with this implementation has been twofold, namely: (1) what boundary conditions to use to couple the solution and (2) how to couple the modes efficiently. The main issue with the one-way NM solution has been what boundary conditions to use to couple the modes, so as to conserve flux in at least some reasonably approximate fashion. It can be shown that neither using pressure or particle velocity solely is satisfactory. The issue is that neither of the two choices conserves flux, which takes a toll in calculating the field out to distances; nor do they agree with Evans’ two-way solution. This indeed is also a problem with the PE method for which some implementations - the pressure conserving type of earlier days - manifested a problem.

The efficient method that is usually implemented in range-dependent NM models consists of using the mean of the two boundary conditions, which is suggested by Evans two-way solution in that the back-scattered return component is dropped. For this approximation the incoming wave in the left segment is assumed to be given, and we require the solution to be purely outgoing in the right segment, which means =0 in Eq. (12). Solving Eq. (12) with the latter assumption, we have for the backscattering amplitudes :

. (18)

Using result (18), we find that forward-going wave amplitudes are given by:

. (19)

The next approximation made is the so-called single-scatter solution. This approximate solution can be obtained by neglecting higher-order terms in the recursion formula (19):

. (20)

It can be shown that the matrix is the arithmetic mean of coupling matrices based on pressure matching and velocity matching.

Thus, Eq. (20) suggests a reasonable accuracy algorithm for mode coupling, which has been implemented in SWAMP. If backscattering effects are not important, which is equivalent to dropping the backward component of Evans’ solution, then this solution will agree with the two way solution of Evans’ out of necessity. The other concern is the time consuming effort required in projecting from one range-independent region to another. If, as is most often the case, the vertical wave functions are made numerically, then one is required to use numerical quadrature in connecting modes through projection integrals (5) and (10), a very time consuming process. In contrast, in SWAMP the projection integrals (7) and (10) for calculation of the solution (20) have closed analytical form, which gives great improvement in speed over numerical quadrature.

To enlarge on the topic of the applicability of the solution in form (20), let us consider the issue of flux conservation across the vertical interface between two range-independent subregions in a one-way approximation. From this point on, the Hankel function asymptotic will be used explicitly and the scaling factor will be omitted. The time-averaged (for harmonic time-dependence) energy flux across the boundary from region I to region I+1 for the one-way equation is, from Eqs. (1) and (9):

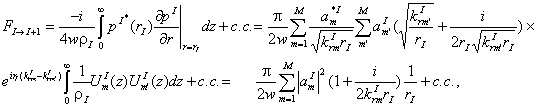(21)

where we have used the orthogonality of the vertical eigenfunctions. c.c. denotes complex conjugate. This means that conservation of flux for any strictly one-way normal mode method, in the event that _, which is usually the case,

. (22)

The boundary conditions requiring flux conservation through the interface suggest that the use of strictly one-way wave equation coupling places severe restrictions on the form of the expansion coefficients that connect the sub-regions. In particular, loss or gain of a mode over an interface - almost always a higher order mode - presents the problem of what happens to the energy. It is either lost or gained by the deletion or addition of the mode. The question of the necessity of including a continuum component with higher angle components, which would more uniformly deal with the addition or subtraction of the propagating mode, can also be a difficulty. Another concern is that when the numbers of modes in adjacent sub-regions are not the same, i.e. , then the energy due to the loss or gain of a mode must be either redistributed within the remaining modes or we can not assume conservation of flux. Indeed, the flux from the loss of a mode would likely be partly dumped into the bottom. The issue of what happens to flux when a mode is gained is subject to further study, but it is likely taken from adjacent modes. However, this development suggests that a strictly one-way wave equation method is not likely a valid method of derivation unless one better understands the two-way problem. This requires that we examine the two-way strategy and determine what this will suggest.

The two-way equation involves both outgoing and incoming waves. The derivation is once again based on the vertical mean flux through a segment. For the backward going or reflected flux we have:

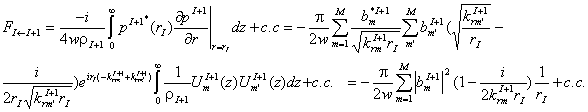(23)

The negative sign simply means that the flux is in the backward direction. The flux in the forward direction for segment (I+1) is likewise:

. (24)

The difference between the two expressions for I=0 is a measure of the variance of conservation of flux that would arise in a one-way expression for just the initial segment. It is clear that for us to ignore the flux due to a reflection (backward going wave), it is required that at the onset and for every segment thereafter the following is satisfied:

. (25)

Thus, Eq. (25) is another physical justification of the validity of Eq. (20), derived from the flux conservation principle.

Let us determine the mechanism of the energy redistribution between modes going from one range-independent subregion to another by equating the mean flux going from region I to I+1. By use of solution (20), we arrive at:

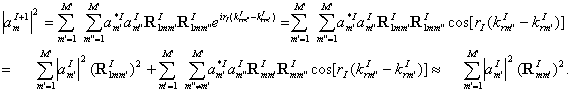
(26)

It is clear that the sine terms sum to zero because they are odd functions and and cover the entire range of allowed values. The cosine terms for large will sum to a small number due to phase averaging, and this result can be understood in terms of the random phase approximation. The approximate expression then gives one an indication of how much of mode m in I+1 comes from mode of I. This leads to an expression for mode conversion. For slowly varying environments the diagonal terms of are large and the off-diagonal terms get progressively smaller as differs increasingly from zero. One may see that for slowly varying environments, energy gets coupled mainly from like modes and adjacent modes. Thus, high modes couple to high modes and low modes couple to low modes but low modes weakly couple to high modes, etc. When one loses a mode, then M ^I+1<M ^I , which is to say that the number of modes in region I+1 is less than that in region I. In that case one loses the contribution of the diagonal term and that component is lost to the bottom, since off-diagonal terms are smaller than diagonal terms and the contribution from those coefficients are the only means by which the lost modes redistribute energy to the remaining modes. To be sure, this must be determined by calculating those terms and by determining the flux lost, but this analysis should give one a good indication of the redistribution of flux on a modal basis. These expressions are also useful for inclusion of fluctuations and may be helpful in determining how energy is redistributed due to fluctuations in the waveguide.

Thus, an advantage of the SWAMP-method is that one is able to calculate the projection matrices in closed mathematical form. This is a major advantage over numerical procedures which would require a great deal of computation time to solve the integrals by creating the wave functions numerically at suitably close spacing and then proceeding with numerical integration.

Not only do we have a fast method to calculate modes within a constant region but in addition, due to the analytical nature of the coupling constants, we are able to couple modes quickly. Since the principle that connects modes deals with conservation of flux, that is no longer an issue for one-way problems. Any concern over pressure conservation can be checked in calculation and is never a problem. Indeed, pressure conservation is only a local problem while flux conservation usually manifests itself over large ranges and is more of a global issue in that equating flux across a boundary is connected with conservation of energy. It must be remembered that conservation of energy is valid under the lossless condition and that both a lossy medium and the possibility that energy may get lost in an infinite bottom would cause a violation of this conservation principle, as it should for such cases. Indeed, the question of mechanisms whereby energy is lost and not that energy is lost is the more relevant. The main concern here is whether one has introduced artificial loss by some numerical device for which some correction is required.

At the end of the discussion of range-dependent normal mode algorithms I would like to mention a further approximation which is often used in normal-mode models. An adiabatic approximation is based on neglecting the cross-coupling terms in integrals (7) and (10), which allow energy from one mode to transfer into other modes. Instead, one assumes that in going from one range to the next the modes will couple adiabatically, i.e., without any transfer of energy to other modes. This approximation was introduced into underwater acoustics by Pierce, based on analogous results for the Schroedinger equation. The final adiabatic formula for the pressure field:

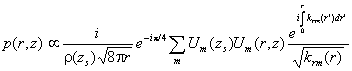. (27)

In practice, the eigenvalues and eigenfunctions are normally calculated at a discrete set of ranges with linear interpolation for intermediate points. The adiabatic approximation gives accurate prediction when the range dependence is sufficiently weak. The mathematical definition of the “weakness” is very difficult to formulate in a general sense. For some environments the adiabatic approximation gives very poor results.

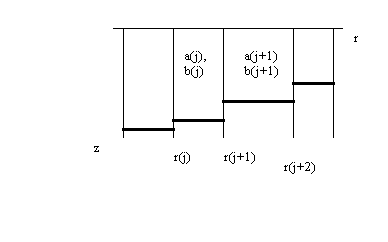
FIGURE 3.2. Schematic range segmentation for coupled normal mode problem.