Loss Mechanisms 

 


In  realistic media it is observed that the sound wave amplitude falls off faster in range than the theoretical  law for lossless waveguides. This effect can be explained by the conversion of some of the acoustic energy into heat due to a variety of mechanisms, which include chemical relaxation in seawater and frictional and viscous losses in the bottom sediment, scattering by ocean waves at the surface, irregularities of the bottom topography, etc..  Each contribution is very small, and  the total influence can be accommodated by introducing a small imaginary part into the sound speed or wave number in the Helmholtz equation:

 .                  (1)

We can derive the relationships between different attenuation units by simply considering a plane wave  attenuated with distance:

 ,                          (2)

where the unit of  is nepers/m, if r is in  meters. The attenuation is often expressed as a loss in decibels (dB) per unit distance:

.                         (3)

In terms of the real and imaginary parts of the sound speed, Eq. (2) can be rewritten as:

        (4)

By comparing (2) and (4), we can conclude:

                                                             (5)

           Very often the attenuation is expressed as a function of  frequency in units of

dB/(m kHz):

  ,                                                           (6)

or as a function of wavelength  in dB/wavelength.  These units are very convenient if we want to make a pulse propagation study.  In these units, it is required that the ratio of the intensities in dB between points one wavelength apart be given by :

  .           (7)

Many studies have been undertaken to find  generalized empirical formulas for  attenuation in the water-column.  One of the most commonly used expressions for the frequency dependence (frequency in kHz) of the attenuation in the water column is:

.       (8)

In the frequency range up to 500 Hz, the attenuation in the water column calculated from (8) is not more than 1 dB/km. At the same time the attenuation due to the interaction with the ocean bottom is on the order of  10 dB/km.

It is still acceptable to use  propagation models based on  zero attenuation in the water column. But it becomes important, especially for  high-order modes and long ranges, to include the loss mechanism due to the interaction with the bottom. However, the eigenvalues would become complex, requiring the use of complex root finder algorithms which are not stable nor efficient. An alternative approach is to obtain the real eigenvalues for the variable sound speed profile in the water column and then to calculate an approximation to the imaginary parts of the eigenvalues using perturbation theory.

To illustrate the technique, let us assume that we know the normalized modal functions   all the way down to the terminating bottom and discrete horizontal eigenvalues   for  a waveguide with arbitrary density, arbitrary sound speed profile in the water-column, arbitrary bottom layering, and zero attenuation.  The zero-superscript in parenthesis should not be confused with the similar one for the iso-velocity case.  and   can be found in the water column, and can be extended to the bottom layers by an inverse iterative procedure. Then we can add an attenuation profile  in the bottom () such that

.                            (9)

The form of equation (9) is very general and allows us to vary attenuation from one bottom layer to another.  In Eq. (9)  is treated as a first-order perturbation to the wavenumber for the lossless waveguide. The next step is to assume that the perturbed wavenumber causes first-order perturbations, and , in the modal eigenfunctions and horizontal eigenvalues, so that we can seek a solution of the form:

                         (10)

for the Helmholtz equation with attenuation:

 .                           (11)

Substituting form (10) into Eq. (11), grouping terms of the same order , we arrive the following equation for the first-order perturbation:

 .                                                                                                                                                                                                                                                                                                                               (12)

The left member of this non-homogeneous differential equation is identical with that of the equation for the lossless problem; hence for vanishing perturbation this leads both to the proper eigenvalue and to the proper eigenfunction , as it must. The theory of  differential equations shows that a necessary condition for the existence of a solution of the non-homogeneous equation is the orthogonality of the perturbation function on the right to the solution of the homogeneous equation :

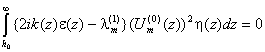    ,                                    (13)

which implies

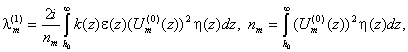             (14)

where  is the normalization factor. The integral (14) can be calculated analytically, because usually  is a constant for a particular layer and  is the exponential functional form for the bottom layers.  is the imaginary part of the horizontal wavenumber which allows us to calculate the exponential decay of the acoustic wavefield due to the interaction with the bottom.