are systems that attempt to negate the effect of gravity (or light) on biological systemsAs long as the response time is less than the stimulation time, the constant changing of the gravity vector prevents a directional response. This concept allows the simulation of gravity levels: If a (small) plant is rotated horizontally at 1- 3 rpm artifical weightlessness (aka microgravity) is simulated. Placing the rotating axis at an angle simulates a fraction of gravity. The residual gravity (simulating e.g. the Moon's gravity of 1/6 g) requires an angle of sin -1(1/6) or ~10 deg. |
|
| Hypergravity can also be simulated! If accelerations (gravity) of bodies larger than Earth are to be simulated a centrifugal force is needed and the clinostat turns into a centrifuge. The force depends on the angular velocity and radius of the device (see Theory). |
|
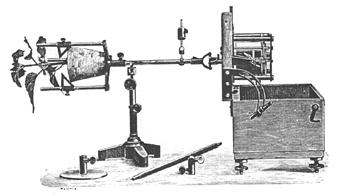 One of the first clinostats. This model was used by Wilhelm Pfeffer (~1900) and is already an improvement (smaller version) of the original machine, which was built by Julius Sachs (~1879) |  A simple but specialized one-axial clinostat that accommodates a Magnetic Field Chamber (shown without cover plate and seed cassettes). This device was used for the preparation of the shuttle experiment on STS-107. |

The most thorough elimination of vectorial (gravitational) effects is achieved with rotation in all possible directions, whichprovides complete randomization of the gravity vector and achieve the best weightlessness simulation. |
 This system has two co-axial drives; the relative velocity between the two wheels determines the clinorotation around the horizontal 'spokes' of the experimental plastic cups. The average speed of the two wheels determines the rotational velocity around the vertical axis. This design provides a smooth transition between clinorotation and centrifugation. Because both clinorotation and centrifugation can be controlled the threshold of force sensitivity can be tested. |
|
The simulation of microgravity depends on a variety of factors, the response time, external factors such as buoyancy, temperature, light etc. If the(gravi)stimulus changes constantly and faster than the response time, the (biological) system is unable to respond to the stimulus. However, the compensation of gravity by rotation must be limited to avoid centrifugal forces that may result in unrelated effects on the system of interest. The figure below illustrates the constraints of rotational simulation. Assuming that the axis of rotation is horizontal, the lines give the limit of the centrifugal force induced by the angular velocity ω (omega) as a function of the radius. As the radius increases the centrifugal force increases and the size of the system becomes a limiting factor. The response time determines the minimal rotational speed (angular velocity). For plants the response (presentation) time is about 1-2 minutes. Because the system integrates the rotation over time, the stimulus in one direction must be less than the time needed for one half revolution. In our example, a plant with a one-minute response time needs to be rotated faster than one half revolution per minute (~0.05 radians per second). |
|
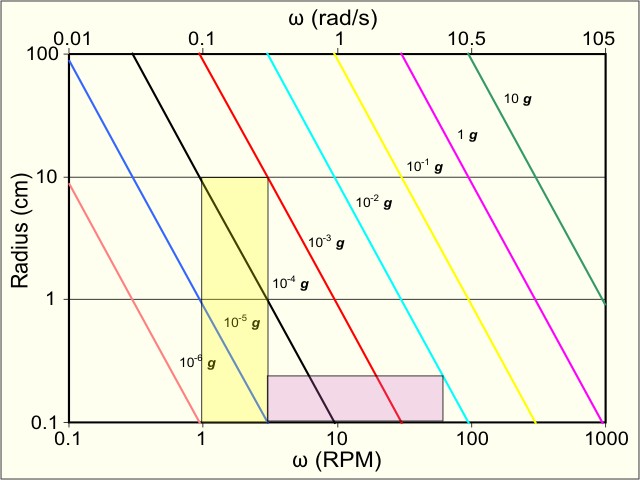 Log/log plot of radius and angular velocity. the different lines define the various g-levels by the centrifugal force. The rectangles exemplify usable radius and velocity ranges for slow (yellow) and fast (pink) clinostats. |
|
|
Therefore typical (slow-rotating) clinostats turn at a rate of 1 to 2 rpm. The physical dimension of the plant (e.g. leaf length) must be less than the predetermined threshold of centrifugation. For a plant with 5 cm long leaves the yellow box describes the usable operating range of a clinostat. In contrast, the so-called fast rotating clinostats operate at rates of 30 to 150 rpm but are restricted in diameter (purple rectangle). These clinostats are often used with liquid systems (algal suspensions), where sedimentation is compensated by faster rotation while maintaining the ‘normal’ interaction of the organism(s) with the(ir) environment. Although rotation leads to compensation of gravity but not microgravity. Because plants sag in response to their own weight, an often underestimated artefact of clinorotation is excessive mechanostimulation. |
|