Chapter 6: Resistance to Extinction(1)
Overview: In the three major sections of this chapter,
we examine the findings and theories having to do with extinction
and partial reinforcement. We start in the first section with an
overview of extinction and related findings and procedures, and examine
some factors that influence how rapidly extinction occurs. Three classical
accounts of extinction are then presented. These include Hull's Drive
Reduction Theory of extinction which claims that extinction involves
a drive component, Guthrie's Contiguity Theory of extinction
in which response competition plays the major role, and finally,
the Mowrer and Jones claim (Discrimination Theory) that extinction
involves learning to discriminate a current no-outcome situation
from the previous response-generated outcome context the organism
found itself in. The second section overviews the partial reinforcement
effect. Various partial reinforcement schedules are discussed
here, as are two popular theories of extinction following partial reinforcement:
the Frustration Hypothesis of Amsel, and the Sequential
Hypothesis of Capaldi. The final section presents and evaluates
the work of people like Hulse demonstrating that animals are sensitive
to global patterns of outcomes.
I. Acquisition of Extinction
What an unfortunate choice of
wording occurs in extinction, and in the ambiguous phrase resistance
to extinction. The word carries connotations of destruction and loss.
Dinosaurs become extinct, never to roam the earth again. So too might we
expect old habits and memories to become extinct, irrecoverable, and irreplaceable.
But that is not what happens in the process of extinguishing an operant
or instrumental response. And for that reason, I've labeled this section
acquisition of extinction: Almost all theorists today regard
extinction as a process of continued learning. At issue is whether
it is the learning to inhibit a response done earlier, the learning
of a new response opposite to or incompatible with that performed
earlier, or the learning that the earlier response is simply no longer
effective.
In short, extinction isn't
the opposite of learning, it is learning. And the fact that it often
seems to involve withholding a response should not mislead you about
that. To remind you, performance is not the same as learning:
What you see (or don't see, in this case) isn't all there is; there
are numerous possible internal mechanisms and reasons behind the actual
observed performance.
A. Preliminaries: Procedure & Relevant Findings
Extinction refers to both a
procedure (actually, several procedures) and a finding. Within the
framework of operant and instrumental conditioning, the typical
procedure is this: Following previous conditioning of a response using
either reinforcement or punishment, the outcome (the reinforcer
or punisher) is removed. And the finding is this: Normally, following
such removal of the outcome, behavior reverts to what it was prior to
the initial learning. How long it takes to do so is referred
to as the response's resistance to extinction.
Some Basic Findings
There are a number of factors
that can influence resistance to extinction (and we will examine some of
these below). But in general, extinction displays the same type of diminishing
returns curve as does acquisition: The bigger changes will occur early
in extinction, and later sessions of extinction will display progressively
smaller changes in the response. Thus, as was true of acquisition, extinction
involves a response being driven towards an asymptotic level of performance.
Moreover, as you may remember,
extinction is also characterized by a phenomenon referred to as spontaneous
recovery: Presentation of the stimulus following extinction
will likely cause momentary and temporary recovery of the response. How
much recovery occurs will depend on several factors. One of these is the
time interval between the last session of extinction, and the current
test of the stimulus: The longer you wait after extinction to test for
spontaneous recovery, the more likely it is that you will obtain it. Another
is the number of sessions of extinction: With repeated sessions
that take the animal close to the extinction asymptote, spontaneous recovery
becomes less likely.
As was true of acquisition,
extinction is characterized by generalization: A response extinguished
in the presence of one stimulus tends not to be observed in the presence
of other, similar stimuli. (Of course, we assume here that the response
was previously given to these, so that we are now seeing something
new.) In this case, the resulting gradient is normally referred to as a
gradient of inhibition.
Finally, following extinction,
relearning of the response will typically exhibit a significant
savings score, consistent with the claim that extinction isn't simple
forgetting. Indeed, theorists such as Rescorla have taken the speeded
relearning as evidence that extinction doesn't technically involve replacing
a response's excitation with inhibition. The argument Rescorla uses is
that a truly inhibited response should pass the retardation test. That
means that it should take longer to learn, resulting in a negative savings
score. Thus, Rescorla views positive savings as evidence that extinction
does not really involve inhibition (as was originally claimed by theorists
such as Pavlov). But because there is a savings, we may at the same time
presume that something of the original excitatory association has remained
in the animal's memory.
But what of the speed of
extinction? Is there anything that might usefully be said about that? In
fact, there is. As you already know from previous chapters, a number of
factors influence the speed of extinction (its resistance). Thus, we read
earlier (Chapters 4 and 5) about the Fowler and Miller and the Baum
studies in which forcing competing responses speeded up extinction.
We also read in Chapter 4 about the Boe and Church study in which
punishment of the response during a pre-extinction 15-minute session speeded
up extinction, the speed-up depending on the severity of the punisher.
In Chapter 5, the Seward and Levy study on latent extinction
was introduced, a study that will prove particularly relevant to evaluating
several of the theories below. To remind you, Seward and Levy associated
a goal box with non-reinforcement, and found that this speeded up extinction
of running to the goal box. And finally, the partial reinforcement effect
was briefly discussed in Chapter 4. In partial reinforcement schedules,
only some responses are reinforced during learning, rather than every single
response. Different partial reinforcement schedules will have differing
effects of extinction, but in general, partial reinforcement will lead
to greater resistance to extinction than continuous reinforcement.
One final preliminary is
worth noting here: With continuous reinforcement, whatever tends to
result in faster acquisition or a higher rate of acquisition during learning
will, paradoxically, result in faster extinction. Both Roberts
and Amsel, for example, have shown that larger reinforcers lead
to faster extinction when they are removed. In like fashion, there are
a number of studies suggesting that greater numbers of continuously reinforced
trials during acquisition will result in faster extinction. Such findings
are at first blush problematic for associationist theories that claim that
larger reinforcers or more pairings result in a stronger association: Shouldn't
a stronger association result in longer-lasting learning?
Alternative Procedures
There are actually a number
of procedures that may be used to lower the expression of a response. One
that you are certainly aware of, for example, is punishment training:
the association of a response with an unpleasant outcome. Although extinction
and punishment at first seem different, there are some strong similarities
between them at an abstract level, especially when we are dealing with
the extinction of a previously-reinforced response. In some sense, we can
think of extinction in this situation as the removal of an expected reinforcer
following a response, and that definition gets us very close to the definition
of negative punishment that we briefly considered in Chapter 4.
On this account, the normal extinction procedure represents a kind of mild
punishment. Of course, we learned earlier in the Boe and Church study that
mild punishers do not work well. However, if you go back to that study,
you will see that mild punishers are as effective as extinction:
They work more slowly than strong punishers, but they eventually do work.
In many studies in which mild punishers have seemed ineffective, they have
failed to be compared to extinction. Perhaps the temporary suppression
of behavior by a mild punisher ought more properly to be compared to the
temporary suppression in extinction. In the latter, as you know from our
discussion of spontaneous recovery, there is also a recovery of
the response, the amount of recovery depending on the amount of time that
has passed.
The point of this discussion,
of course, is to broaden our horizons about how to think of extinction.
If we regard extinction as the loss of an expected outcome, then there
are really a number of procedures that may fit this definition in addition
to punishment training and simple loss of the outcome. We can add to our
list omission training, for example, in which we typically require
an animal to withhold a response that has previously been associated with
reinforcement. In the typical omission training procedure, unlike the two
procedures mentioned above, we actually now reinforce the animal for not
responding. An example is the Sheffield experiment described in
Chapter 4, in which dogs were rewarded for not immediately drooling in
the presence of food.
Another procedure we came
across in the last chapter (in the discussion on Premack) was to follow
a strong response (a preferred response) with a weaker (less preferred)
response. That procedure by itself doesn't easily fit the portrait of extinction
we are starting to build up. But if you now re-analyze this situation from
the point of view of Timberlake and Allison's response deprivation hypothesis
(the equilibrium theory), you can see that this procedure
deliberately throws the weak response out of equilibrium: The procedure
moves the weak response well above its bliss point. Having a response
out of equilibrium is a type of punisher, so that we would now expect the
animal to moderate the expression of the stronger response down, in order
to find the best compromise for how often these two responses are performed
(i.e., the point nearest their joint bliss point). Indeed, you may
wish to consider what the Timberlake and Allison theory might have to say
about following a response with a punishment such as shock. Shock certainly
has to be an activity that occurs well above its bliss point in this type
of experiment, resulting in strong pressure to moderate the shocks downward.
Thus, certain types of experimentally induced disequilibrium can result
in smaller levels of responding.
A final procedure that we
can discuss here involves simply removing the contingency between the response
and the outcome. That is, we move the animal to some point on the diagonal
in the optimal contingency space. On the diagonal, the probability
of an outcome is the same whether the animal makes or withholds the response,
resulting in a zero contingency between the response and the outcome.
To remind you, Hammond found that rats that had learned a response
ceased making the response once the contingency became zero. Normally,
procedures such as omission training and establishment of a zero contingency
result in a slower build-up of non-responding compared to the typical extinction
procedure, but over the long haul, they appear to be as effective as extinction.
Now that we have discussed
some of the preliminaries, let's move on to some of the classic theories
of extinction.
B. Hull: Extinction & Drive Reduction
We discussed Hull's Drive-Reduction
Theory of learning in the last chapter. For extinction, three points will
be important to remember. The first is that Hull distinguishes between
two types of association between a stimulus and a response. One is excitatory,
and the other inhibitory. The second point to remember is that Hull believes
extinction is a form of learning in which the inhibitory link or association
increases in strength. And the third point is this: Because learning in
Hull's system only occurs when there is drive reduction (alternatively,
lessening of the drive stimuli), then there must be some sort of drive
reduction in extinction. Or put another way: Even though the obvious reinforcement
has been removed in the typical extinction procedure, somewhere, somehow,
there is still a reinforcer. The question then becomes, what is that reinforcer?
Formulation Of The Theory
Let us start with the notion
of two associations, one excitatory; the other, inhibitory. The excitatory
association is SHR, of course, the habit
strength between a stimulus and a response. The inhibitory association,
by contrast, is SIR, which Hull termed conditioned
inhibition. At the start of learning (and generally, until after the
extinction procedure has started), SIR is
at zero.
But you will recall that
there were two types of inhibition in Hull's system. The other type of
inhibition was not learned. This type Hull called reactive inhibition,
or IR. Do note that there is no subscript for the stimulus
in the formalism for reactive inhibition. That is because reactive inhibition
doesn't depend on the stimulus at all. Rather, reactive inhibition is a
type of fatigue or resistance that occurs with the performance of a response,
and that makes that response a little bit less likely to occur in
the immediate future. Normally, during initial learning, the presence of
a reinforcer increases the habit strength, so that we get boosts in both
SHR and IR. But the bigger
boost presumably occurs in SHR, which means
that excitation will be larger than inhibition. So long as that is the
case, we would expect to see continued responding during learning, even
though we may presume that there is a lot of reactive inhibition about,
if the learning trials are spaced relatively closely together.
Fatigue, however, is something
that we recover from by resting. In like fashion, Hull claimed that reactive
inhibition would fade away when the animal had a chance to rest from doing
the response. So, in any given situation, the amount of reactive inhibition
would depend on how long ago the animal had responded.
That brings us to the normal
extinction procedure, in which we remove the reinforcer. Once the reinforcer
is gone, SHR no longer increases. But as the
animal keeps responding, reactive inhibition keeps increasing, until finally,
the total amount of reactive inhibition exceeds the amount of excitation.
And when that happens, by the principle of algebraic summation (i.e.,
effective reaction potential), the animal ceases to respond.
There is a sense in which
this should remind you of the approach-avoidance situation we discussed
earlier. Like Hull, Dollard and Miller claim that a response can
be associated with both excitation and inhibition. And like Hull, they
claim that whether the animal makes or withholds the response (runs towards
or away from the goal in the example from Dollard and Miller in Chapter
4) depends on algebraic summation. But unlike Hull, their avoidance gradients
(inhibition) don't change with rest.
An illustration might be
useful at this point. Figure 1 shows some sample results that represent
what might happen at various stages during extinction. In each case, the
light blue bars (the ones with the letters in them) represent the habit
strength, or SHR . These bars are identical
to one another: They represent how strong the habit strength is, going
into extinction. Because there is no more reinforcement, the habit strength
will not change.
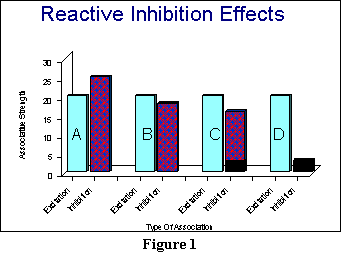 The first two bars (the A pair) are meant to capture roughly what
happens well into extinction, at a point where the reactive inhibition
has built up dramatically. (Reactive inhibition in Figure 1 is represented
by the patterned bars: the purple bars, for those of you with a color monitor.)
In this case, the reactive inhibition has increased past the level of excitation.
Now assuming (for the sake of argument) that D and V and
K are all equal to 1, then the animal should no longer respond at
this point: Inhibition should be greater than excitation, so that there
will be a negative effective reaction potential.
The first two bars (the A pair) are meant to capture roughly what
happens well into extinction, at a point where the reactive inhibition
has built up dramatically. (Reactive inhibition in Figure 1 is represented
by the patterned bars: the purple bars, for those of you with a color monitor.)
In this case, the reactive inhibition has increased past the level of excitation.
Now assuming (for the sake of argument) that D and V and
K are all equal to 1, then the animal should no longer respond at
this point: Inhibition should be greater than excitation, so that there
will be a negative effective reaction potential.
However, since the animal
at Point A stops doing the response (and starts resting those muscles
associated with that particular response), the reaction inhibition now
has a chance to start fading away. Thus, after a relatively short while,
reaction inhibition will decrease to the point that inhibition is now slightly
less than excitation. That point is represented by the B bars (the
second pair of bars) in Figure 1. Note that excitation is stronger, so
we would expect the animal to start responding again (because the effective
reaction potential in this example has now gone positive).
One more point is important
about what happens at B: Hull considers reactive inhibition to be an
unpleasant drive state. And as you can see in comparing what happens
to inhibition at Points A and B, there is drive reduction.
Thus, we have met the condition that there be some sort of reinforcer present
for learning during extinction. That reinforcer is the decrease
in reactive inhibition over time. But note that this decrease occurred
because the animal performed a response that allowed the reduction in reactive
inhibition. What was that response? Quite simply, the response of not
using the particular muscle movements it had been executing earlier. We
will call this the response of not responding, for short. Thus,
at Point B, the animal is reinforced for not responding, because
the reactive inhibition has lessened a sufficient amount.
The response of not responding
is what Hull has in mind when he speaks of conditioned inhibition.
Please understand that this conditioned inhibition is not a drive
state, unlike the reactive inhibition. Instead, it is a learned association
between the stimulus and a response that essentially teaches the animal
not to do that response. Thus, a little bit later, at Point C, the
total inhibition the animal will have can be represented by the amount
of reactive inhibition it still has left, and by the amount of conditioned
inhibition it has now acquired. I have represented conditioned inhibition
with the dark region of the inhibition bar in C. As you can see,
there is a bit of conditioned inhibition here, but much more reactive
inhibition. However, since the total inhibition is less than the excitation,
we would expect the animal to start responding again at Point C.
If, however, we have removed the animal from the experimental apparatus
so that it cannot make the response, then with additional time (and
rest), the reactive inhibition should have totally dissipated, leaving
only the conditioned inhibition behind. This situation is represented by
the D pair of bars. At Point D, there is a great deal of excitation,
and some conditioned inhibition. Thus, when we decide to return
our animal to the apparatus, the animal should start the process of (futilely)
making the response anew. Like excitation, conditioned inhibition can
never decrease.
You can work out from this
example what should happen next. The animal keeps responding until reactive
inhibition builds up so that total inhibition (reactive and
conditioned) exceeds excitation. Of course, less reactive inhibition
will be needed for a negative effective reaction potential than previously,
because there is some conditioned inhibition present. In any case, when
the inhibition builds up to sufficiently high levels, the animal stops
responding. That results in a further opportunity for drive reduction,
which, in turn, increases the total amount of permanent, conditioned inhibition.
This cycle continues until conditioned inhibition is always higher than
excitation. At that point, extinction has been successfully completed.
Some Compatible Predictions
There are a number of findings
that are compatible with this approach to extinction. Some of these we
have discussed previously. Among these is the spacing effect. To
remind you, the spacing effect refers to whether initial learning involves
massed practice in which there is very little break between trials,
or spaced practice in which the animal rests a bit before going
on to the next trial. All other things being equal, spaced practice
results in significantly better learning.
You can probably figure out
why Hull's model is compatible with this approach. Reactive inhibition
should occur each time the animal responds in either condition. But in
spaced practice, there is time for the reactive inhibition to decrease
between trials. So, by algebraic summation, there should be relatively
more net excitation in spaced practice, resulting in a stronger response.
There is another finding
arising from the spacing effect that also fits this model. For this finding,
we will restrict ourselves to a condition in which we put our animals through
just massed practice. Following the end of the practice session,
there is a tendency for the response to get stronger with time. The diagram
for this experiment would be something like the following:
Group Initial
Learning
Response Tested At
1
massed practice
5 sec after practice
2
massed practice
30 min after practice
Here, Group 2 will show a stronger response, even though both groups
have had the same initial learning. This finding is called the reminiscence
effect. The reason it fits Hull is that Group 2 has had an additional
30 minutes in which to allow reactive inhibition to go away. So, its relative
excitation (effective reaction potential: excitation minus inhibition)
will be stronger.
A second compatible finding
is spontaneous recovery. If you go back to Figure 1, you can see
why spontaneous recovery should occur by comparing relative excitation
at Points A and B. At Point B, the reactive inhibition has decreased past
the excitation, so that the response is now positively excited once more.
In general, when we think we are at extinction, there is a little bit of
reactive inhibition on top of a large amount of conditioned inhibition,
and when that little bit of reactive inhibition goes away, the conditioned
inhibition may be below the conditioned excitation. To give you a feel
for this, spontaneous recovery reaches a maximum several hours after extinction,
and may then persist for several days. Indeed, Mackintosh and others
have found that the amount of spontaneous recovery can be quite substantial
(see also a recent interesting simulation of this effect by Dragoi and
Staddon).
Of course, it is possible
to get rid of spontaneous recovery, but the procedure that is normally
required involves successive sessions of extinction. If you think
about what goes on in successive sessions, you will realize that each session
builds up more and more conditioned inhibition, so that each succeeding
session will require less and less reactive inhibition before the animal
stops responding. Our prediction here is that spontaneous recovery should
decrease over repeated sessions (it does!) until, finally, there
is no spontaneous recovery because conditioned inhibition always equals
or exceeds excitation.
A third set of findings involves
the effort or strength required to make a response: The more effort is
required, the faster the extinction will be. From the standpoint of Hull's
theory, greater effort will fatigue the muscles more, resulting in greater
reactive inhibition.
One more compatible finding
may be mentioned. If we compare the normal extinction procedure with the
procedure of moving the animal to a zero contingency (as in Hammond's
study), we find initially slower extinction in the latter. This is also
consistent with Hull, at least at broad scale: A zero contingency means
that there will be some random pairings of a response with drive
reduction. Thus, conditioned excitation no longer stays at the same level
in this procedure. If excitation is rising along with inhibition,
then we would certainly expect extinction to slow down compared to the
usual procedure.
Incompatible Findings
I earlier wrote that the
Seward and Levy study would prove important for evaluating a number
of theories. Here is our first test case. They set up their experiment
as follows:
Group
Phase 1
Phase 2
Phase 3
Experimental run to goal
in goal with no RF extinction
Control
run to goal
extinction
And what they found, of course, was that the group with the experience
of being placed in a goal box that no longer delivered food extinguished
more rapidly. Apparently, their process of extinction had already started
in Phase 2.
So why is this finding problematic
for Hull? The answer will turn out to be quite similar to the reason Light
and Gantt's finding (the study on classically conditioning paw withdrawal
in temporarily paralyzed dogs) was problematic for Hull's theory of classical
conditioning. For Hull, a response has to be made in order for learning
to occur. And specifically with respect to extinction, a response
has to be made in order for there to be a build-up of reactive inhibition.
But the animals in Seward and Levy's experimental group did not
make the response of running to the goal box. Therefore, that response
could not have become associated with IR.
A similar type of finding
occurs in a study by Heyes, Jaldow, and Dawson. They did an experiment
on observational learning in which one group of rats saw another
go through extinction (i.e., our group saw the others perform a response
they had also learned, but they also saw that the response longer resulted
in reinforcement). As you might expect from the discussion of vicarious
punishment in the previous chapter, the observational group exhibited
faster extinction. But as in the Seward and Levy study, the observational
group had apparently started the process of extinction before ever making
a non-reinforced response. They should not have had any reactive inhibition
from simply observing other rats. Hull would therefore have a great deal
of difficulty explaining this finding. As you may imagine, there are now
a number of studies that employ some variant of a procedure in which extinction
can commence in the absence of an overt, physical, non-reinforced response
by the animal.
A third class of findings
concerns the partial reinforcement effect. Normally, animals on
partial reinforcement exhibit slower extinction. However, Hull would predict
the exact opposite finding, as continuously reinforced animals have had
more trials involving drive reduction, and thus, should have a much stronger
habit strength.
Finally, a related problem
for Hull involves the fact that extinction in continuously reinforced
animals appears to be inversely related to the number of acquisition
trials. For Hull, having a large number of reinforced trials should mean
having very strong habit strength, so that a very high level of inhibition
will be needed before the animal stops responding (i.e., before the inhibition
equals or exceeds excitation). However, quite the opposite effect tends
to occur: Large numbers of continuously reinforced trials appear to result
in faster extinction rather than the predicted slower pace.
You already know of the numerous
problems that Hull's theory of excitatory learning ran in to; those problems
combined with the issues mentioned above were sufficient to send theorists
scurrying for another explanation.
C. Guthrie: Extinction & Response Competition
Guthrie's theory of extinction
can essentially be presented in a sentence or two. It will help to see
his theory illustrated graphically. Figure 2 presents a part of the theory
as we have discussed it in the previous chapter. In this figure, we will
not concern ourselves with the issue of the many, many contextual stimuli
to which a response may become associated. Rather, let us assume one effective
stimulus that will eventually become conditioned to the response we desire.
That stimulus is the light blue oval in the top left-hand portion of the
figure. As you can see from this figure, it becomes associated with a variety
of responses, each of which overlays the preceding response. That is meant
to suggest the operation of response competition. By the principle
of postremity, of course, the response on top of the pile (the most
recent response) is the one that is most probable when the animal
is once more exposed to the stimulus. (You may wonder why, if that response
is most probable, other responses can eventually overlay it. The answer
in part is that while it is indeed the first response likely to
be given when the animal is once more exposed to the stimulus, it is not
the only response that will occur in the presence of that stimulus.
Once the animal has given that response, it may give another which now
can become conditioned to the stimulus, thus in turn becoming the most
likely response.)
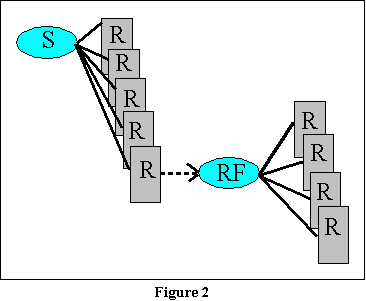 In any case, once the response we are interested in is emitted by
the animal, a new stimulus (the reinforcer indicated by the second
oval) enters into the context. And as you can see from this diagram, the
responses that condition to this new stimulus do not overlay the previous
response that led to it (bar pressing, for example).
In any case, once the response we are interested in is emitted by
the animal, a new stimulus (the reinforcer indicated by the second
oval) enters into the context. And as you can see from this diagram, the
responses that condition to this new stimulus do not overlay the previous
response that led to it (bar pressing, for example).
So, there is nothing magic
about reinforcement in Guthrie's theory. Indeed, any significant stimulus
that causes the animal to orient to it should have had the same effect,
and not just those stimuli that involve food or drink.
Given this, Guthrie's theory
of extinction is simply as follows: When a given response no longer leads
to reinforcement, other responses may now be made after it that will overlay
(and thus compete with) it. Accordingly, the principle of postremity will
now support the expression of the later responses. Thus, much as did Hull,
Guthrie believes that extinction is also learning. But, it is the
learning of new responses that will compete with the old response. Remove
the second oval in Figure 2, and you now have the opportunity for a very
long deck of responses in which bar pressing is somewhere in the middle,
instead of on top.
The principle of response
competition is an important one, although many theorists feel that response
competition needs to be associated with further mechanisms such as frustration
(see the discussion of Amsel's theory below). Nevertheless, there
are a number of studies that support the idea that competing responses
will speed extinction. We have already briefly read about the Baum
and the Fowler and Miller studies at the beginning of this chapter.
To remind you, Baum looked at the course of extinction of an avoidance
response. In one experiment by Lenderhendler and Baum, rats were
flooded with danger signals during extinction, because they were
physically prevented from leaving the area where they had previously been
punished. In this situation, as you may remember from our discussion of
learned helplessness, they tend to freeze after a few seconds. Freezing,
of course, isn't a competing response, as Maier demonstrated: It
is an SSDR to a danger signal. But what Lenderhendler and
Maier did was to force the rats to move around a bit by pushing them. That
act should result in competing responses being emitted, since it forces
a variety of behavioral responses out of the animals. Consistent with Guthrie's
theory, rats forced to move displayed faster extinction.
Similarly, in the Fowler
and Miller study, rats entering a goal box were shocked either on their
front paws, or on their rear paws. Shock at the rear causes forward
movement which is compatible with the response of moving forward
to the goal; shock at the front causes backward movement which is
the opposite of the response of moving forward. Note in this
experiment that both groups of animals are receiving the same shocks, and
that both groups of animals could have avoided these shocks simply by refusing
to enter into the goal area. Nevertheless, the results were consistent
with the principle of competing responses: The front-shock group extinguished
more rapidly.
An experiment by Adelman
and Maatsch also well illustrates the effect of response compatibility.
In their study, rats were trained to run to a goal box, as in the Fowler
and Miller study. However, during extinction, one group of rats had to
go back into the alley to be removed from the maze, whereas a second group
had to jump over a hurdle from the goal box into a further portion of the
maze to be removed. Much as in the Fowler and Miller study, one group thus
performed responses that were incompatible with the original response (going
back versus going forward), but the other performed responses that were
compatible (both involving going forward). As you ought by now to expect,
the group that had to continue going forward took longer to extinguish.
From the latter two studies,
in particular, we can derive an important point: Only some of the responses
acquired later will be competing responses. It is possible for an animal
to acquire a series of compatible responses that effectively maintain its
performance because they include important components of the earlier response,
or because they essentially constitute a minor modification or elaboration
of the earlier response, or because they may be expressed simultaneously
with the original response.
Despite the successes of
competing response theory, however, there are also indications that additional
factors will need to come into play. Scavio, for example, trained
rabbits with the nictitating membrane paradigm in classical conditioning.
The rabbits learned to blink to CS1 because CS1 had been paired with a
mild shock administered near the eye. Later, Scavio found out that presence
of CS1 interfered with rabbits learning to move their jaws to food
in the presence of another CS. (This involves the summation test
we learned about earlier.) The reason this poses a problem for Guthrie
is that jaw movement and eye blinking are not competing responses:
It is possible to do both at the same time. Of course, the shock UCS and
the food UCS may involve very different, competing emotional states,
but competing emotions were not what Guthrie's theory was about.
A final point concerning
Guthrie's theory is that the Seward and Levy study on latent
extinction and the Heyes et al. study on observational learning
are, strictly speaking, not completely compatible with Guthrie. Regarding
the latter study, animals that are observing other animals go through extinction
aren't really making competing responses (at least, any more than animals
watching other animals go through acquisition), so that they ought not
to have a headstart on extinction. (There is an interesting empirical question
here that Bandura's theory suggests: Does vicarious punishment result in
differential behaviors in the observing group while it observes?
That is, can we build a theory in which watching others go through extinction
increases our activity at that moment, so that new responses may be associated
with the observable stimuli?) And regarding the Seward and Levy study,
animals temporarily placed in a goal box without food might be acquiring
competing responses having to do with the stimulus complex of being
in the goal box, but no competing responses are being associated with
the start box or the alley to the goal box, since the animals are not placed
in that portion of the maze.
The notion of competing responses
is certainly important, but contrary to Guthrie, it is not the sole explanation
of extinction.
D. Mowrer & Jones: Extinction & Discrimination
A third approach to extinction
has been championed by a number of people in a number of different theories
(indeed, the principal theories of partial reinforcement we will look at
below fit within this camp). It is that the time course of extinction depends
on the similarity of the learning and extinction contexts.
Mowrer and Jones's theory,
the Discrimination Hypothesis, is a good sample representative of this
group. According to Mowrer and Jones, the animal in extinction essentially
has to learn that this is a new stimulus condition for which a different
response is appropriate. Put that way, the animal has to learn to discriminate
between the learning stimuli and the extinction stimuli. However, one of
the findings that we know from the literature on generalization and discrimination
is that ease of discrimination between two stimuli will be inversely
related to their similarity. Greater similarity results in greater
generalization, which makes learning the discrimination more difficult.
You can, if you wish, come up with a variety of reasons why similar stimuli
ought to yield greater difficulties in discrimination learning (see also
the next chapter). Perhaps they are simply much harder to tell apart, so
that the animal has to spend additional time orienting to subtle differences
between them. Alternatively, from a Hullian point of view, perhaps the
greater generalization means a higher level of conditioned excitation that
requires extended training to overcome (i.e., more trials to build up sufficiently
high levels of conditioned inhibition). The precise reason for the finding
is less important, at the moment, than the general principle that similarity
will influence rate of extinction.
An obvious test of the Discrimination
Hypothesis is to vary the similarity of learning and extinction, in order
to see whether greater differences lead to faster extinction. (Guthrie
would make the same prediction, by the way; can you figure out why?) A
good example of this type of study involves an experiment by Welker
and McAuley. They trained four groups of rats to bar press in a Skinner
box. All groups were trained in the same way, and the training involved
both being transported to the experimental apparatus in the same
fashion, and being surrounded by the same types of contextual cues
once in the Skinner box. In terms of mode of transportation, the rats first
had the water bottles removed from their home cages, and then had the cages
placed on a trolley with a paper liner. In the Skinner box itself, there
were wood shavings on the floor; a lighted circle above the bar; and a
continual noise in the background.
The four groups of rats were
then put through extinction procedures, but their extinction procedures
differed. Essentially, the design for extinction was as follows:
Group Extinction
Procedure
1
no more RF
2
new transportation; no more RF
3
new box cues; no more RF
4
new transportation & box cues; no RF
The new box cues involved
the disappearance of the noise and the light, and the use of a paper liner
at the bottom of the Skinner box rather than wood shavings. Similar changes
were implemented having to do with the stimuli involved in the transportation
method. Welker and McAuley found the fastest extinction for the groups
with the new box cues (Groups 3 and 4), and the slowest extinction for
the group that just had the reinforcer removed (Group 1). The group with
the new method of transportation (Group 2) was in between these.
There is a certain sense
in which the Discrimination Hypothesis is similar to an important theory
having to do with human memory. This is Tulving's Principle of Encoding
Specificity (see Chapter 8). According to Tulving, when we form memory
episodes, we also include information about the environmental cues that
were present at the time of the event. Remembering in part involves using
probes or retrieval cues that will prime or activate
the appropriate memories (remember the discussion of Wagner's model
of classical conditioning!) The best retrieval cues, of course, will be
those that are actually part of the episode or memory. Thus, Tulving points
out that memory ought to be most successful when we are in an environment
similar to that in which we originally learned. The reason is that by looking
around us at the environment, we should already be activating some of the
environmental cues that were earlier included in the memory. So, there
is a similarity principle here that states that similarity of learning
and retrieval contexts will facilitate recall.
Let us now coordinate this
principle with the Discrimination Hypothesis. If the environment the animal
finds itself in is completely different, then we would not expect
any memories of a given response to be activated that would result in performance
of that response. In this sense, there will be no need to learn to extinguish
the response, because it is simply not elicited by the environment. But
as the extinction environment becomes more similar to the original learning
environment, the memories of what the animal did earlier are more likely
to be primed. Extinction in this sense involves acquiring new memories
that activate a different response. Thus, how strongly a given environment
activates old memories of responding can be taken as a rough guide to how
much interference there will be with learning a new response.
We can perhaps capture the
relationship between these two compatible approaches by stating that Tulving's
theory has to do with how easy it is to remember in similar
contexts, and Mowrer and Jones's theory has to do with how hard
it is to suppress or overcome those memories in similar contexts.
There is an important lesson
here for you in Tulving's work. When you take an exam, try to reinstate
the context in which you originally studied the materials. Thinking about
that context or environment may help provide you with appropriate retrieval
cues. We will see in a later chapter that this is a powerful technique,
and you will learn about a number of studies that support it. In the meantime,
it is a principle you can put to work.
Back
to Mowrer and Jones's theory: Note that this theory in principle can also
explain the effects of large reinforcers during initial continuously reinforced
learning (e.g., Roberts's finding that large reinforcers lead to
faster extinction). A standard experiment on reinforcement size effects
would involve a design such as the following:
Group Acquisition
Phase
Extinction Phase
1
small reinforcement no
reinforcement
2
large reinforcement no
reinforcement
I have included this design because it makes obvious the change in similarity
between the two groups in the acquisition and extinction phases. You need
to think of a reinforcer as one of the stimulus elements that define the
context in which responding is maintained. Within this framework, a
small reinforcement is more like no reinforcement than a large reinforcement
is. Our prediction from the Discrimination Hypothesis would thus be
one of greater resistance to extinction in Group 1, precisely the result
that Roberts and others obtain.
As a final example of work
compatible with this theory, we may consider a study by Dyal and Sytsma.
They ran four groups of animals, three of whom had some exposure to partial
reinforcement (recall that the partial reinforcement effect predicts
greater resistance to extinction in partially reinforced groups). In all
groups, there were two sessions of reinforcement-based learning, but two
of these groups had a session of continuous reinforcement, and a session
of partial reinforcement. These two differed in which came first. The issue
Dyal and Sytsma looked at was whether order of the sessions would influence
speed of extinction.
Here is their design:
Group Session
1
Session 2
Session 3
1
continuous RF continuous RF
extinction
2
partial RF
partial RF
extinction
3
partial RF
continuous RF extinction
4
continuous RF partial RF
extinction
Note that Groups 3 and 4
have exactly the same amount of partial reinforcement during learning.
If all that is important in the partial reinforcement effect is the number
of partially reinforced trials, then we would predict that they ought to
be identical, and show greater resistance to extinction than the continuously
reinforced group (Group 1), though perhaps not as much resistance as the
group with the most partial reinforcement (Group 2).
Can you predict what happened,
and why it fit the predictions of discrimination theory? First, the usual
partial reinforcement effect did occur in the first two groups: Group 2
showed greater resistance to extinction than Group 1. Although we have
not discussed this explicitly until now, that also fits the Discrimination
Hypothesis, since partial reinforcement (in which there are some trials
with no reinforcement) is more like extinction (in which all trials have
no reinforcement) than continuous reinforcement is. And second, Group 4
had a stronger partial reinforcement effect than Group 3! You can
see why this result would be expected from the Mowrer and Jones theory
by comparing Sessions 2 and 3 in the design above: Group 3's Session 2
was reasonably different from their Session 3, making it reasonably easy
to tell the two apart. However, Group 4's Session 2 was similar
to their Session 3, making it harder to tell them apart. As this study
clearly shows, there is more to the partial reinforcement effect than
simply determining how many trials of partial reinforcement the animal
had.
As you can see, the Discrimination
Hypothesis has a number of appealing features. It can account for reinforcement
size effects, and more to the point, the partial reinforcement effect.
It can handle other findings relating to extinction, as well. For example,
animals who have been trained with delayed reinforcement have greater
resistance to extinction. (One could argue that extinction involves a very,
very long delay of reinforcement, so that increasing delays during learning
make the acquisition phase more similar to the extinction phase). However,
more specialized versions of the theory have been developed to account
for a broader range of findings in partial reinforcement, and we turn to
these next.
II. Extinction & Partial Reinforcement
The partial reinforcement
effect (sometimes abbreviated PREE) is the finding that not
reinforcing all correct responses during learning results in longer-lasting
learning. It has been one of the milestones of Skinner's career, and indeed,
much of what we know about partial reinforcement arises from work in his
lab. It is a landmark phenomenon that will separate theories of extinction
into the plausible and the no longer possible. Today, theories of extinction
(like Hull's) that fail to account for partial reinforcement effects are
simply not regarded as viable, even though it is possible in principle
to have different explanations of extinction for continuously reinforced
and partially reinforced learning.
A. Humphrey's Paradox: The Partial Reinforcement Effect
The partial reinforcement effect
has a venerable history. It may surprise you to know that Pavlov
did some early experiments using partial reinforcement in classical conditioning.
Most of what we know about partial reinforcement, however, comes from instrumental
and operant conditioning.
One of the first psychologists
to report the partial reinforcement effect was Humphrey, and it
became known as Humphrey's paradox. It initially puzzled a number
of theorists for the simple reason that everyone at the time believed that
more pairings of a response with a reinforcer ought to result in a stronger,
more lasting association. Thus, the paradox Humphrey discovered was
that under certain circumstances, less was more: Fewer reinforcers could
eventuate in an apparently more durable association.
Although Pavlov did indeed
look at partial reinforcement trials in his work, the status of partial
reinforcement effects in classical conditioning today remains inconclusive.
The results of studies in classical conditioning are contradictory, and
it may be safest to conclude that partial reinforcement here (in which
the CS is only sometimes paired with the UCS) has, at best, weak effects.
Thus, partial reinforcement effects seem to constitute an area in which
classical and operant conditioning tend to yield very different findings.
Before we go on to specific
theories and findings, one more point is worth mentioning: There are indeed
reports of the occasional reverse partial reinforcement effect (or
reverse PREE), in which partial reinforcement will actually cause
faster extinction. There is an interesting article by Nevin
that discusses this, and the upshot (although we will certainly see some
exceptions below!) appears to be that a partial reinforcement effect is
more likely when there have been a relatively large number of acquisition
trials, but a reverse PREE becomes possible when there are only a small
number of trials. You may wish to keep this finding in mind as you evaluate
the theories and findings below.
B. Partial Reinforcement Schedules
Much of what we know about partial
reinforcement today arises from the pioneering work that was done by Ferster
and Skinner, published in their book Schedules of Reinforcement
in 1957. In accord with Skinner's anti-theoretical position, the focus
in this book was more on empirical results than possible underlying explanations
for those results. The work examined the effects of different types of
patterns of reinforced and non-reinforced trials (referred to as schedules).
In any case, many different types of schedules have been examined since
then. We will start with simple schedules.
Simple Schedules
A number of simple schedules
have been proposed, but most people really concentrate on four simple schedules.
These four schedules may be defined in terms of two broad dimensions.
The first dimension involves repetition. We can have a pattern of
events that constantly recycles or repeats, in which case the schedule
is referred to as a fixed schedule. Alternatively, we can have a
random pattern in which there is no systematic repetition. The latter is
referred to as a variable schedule. Note that fixed schedules in
theory may be predictable (that is, the animal or human might
be able to develop an expectancy concerning when a response will be reinforced),
whereas variable schedules are, by definition, unpredictable. (Well, to
be more accurate, they are not successfully predictable: Many people
who play slot machines mistakenly think they can predict the machine's
behavior!)
The second dimension relevant
to defining simple schedules involves what must happen for a response to
be successful in obtaining an outcome. We can refer to this dimension as
the response criterion. By criterion, I mean what has to happen
before the response in order for it to work. In one set of schedules,
the criterion or rule involves the number of responses that have
gone on before. This involves a response-dependent rule: A certain
number of responses, on average, has to occur before a reinforced response.
This type of schedule is referred to as a ratio schedule. Alternatively,
a criterion may involve a time-dependent rule: A certain amount
of time, on average, has to pass before a response will work. Those types
of rules involve interval schedules. When we combine these two dimensions
in all possible combinations, we obtain the four simple schedules outlined
in the table below:
________________________________________________________________
Criterion
_________________________________________________
Repetition
Response Dependent
Time Dependent
________________________________________________________________
Fixed
fixed ratio schedule
fixed interval schedule
Variable
variable ratio schedule
variable interval schedule
________________________________________________________________
Let's discuss each of these
schedules in more detail. The easiest of these to start with is the fixed
ratio schedule (often abbreviated FR). In a fixed ratio schedule,
the animal needs to perform a certain number of responses (the ratio)
in order to get its reward. Actually, continuous reinforcement is
a special case of a fixed ratio schedule, except that it is a fixed ratio
1 schedule (FR1), meaning that the animal needs to emit one response
(the correct response, of course!) to get its reward. In like fashion,
a pattern in which the animal has to make two responses to get a
reinforcement is an FR2 schedule. The number following the FR tells you
which response gets the reinforcement, and how many responses before that
have gone unreinforced. Thus, in FR357, the 357th response works,
but the animal has had to make 356 earlier responses that did not lead
to any reward. As you might imagine, the schedule becomes harder to learn
as the number goes up. Typically, with very large ratios, we have to wean
the animal towards the ratio; that is, we start with much smaller ratios,
and slowly increase the number of non-reinforced trials.
As a rule, higher ratios
result in greater resistance to extinction. So, we would expect more
resistance with an FR300 than an FR20 schedule, for example. Based on what
you know about Mowrer and Jones's Discrimination Theory, you ought
to be able to predict this result.
There are many examples of
fixed ratio schedules in the real world. In many book or CD clubs, for
example, if you buy a certain number of books or CDs, then you get a free
book or CD. Similarly, in a work environment, salary incentives based on
sales could be considered an example of a fixed ratio: A bonus for every
5 sales concluded would be an FR5 ratio, for example. Piecemeal work also
fits this category, when the salary depends on how many pieces are finished.
In a variable ratio schedule
(abbreviated VR), on the other hand, the precise response
that will obtain the reinforcer is not easily predictable. Rather, there
will be a certain average number of responses that have to be made. So,
a VR3 schedule means that, on average, 1 out of 3 responses will work,
though it won't be every third response, as it would have been in the FR3
schedule. Variable ratio and fixed ratio schedules that have the same
number will have the same overall density of reinforcement: They will
have the same numbers of reinforced and non-reinforced responses, but not
at the same places. Thus, below are a sample FR3 and VR3 schedule (in which
the R and N stand for reinforced and non-reinforced responses,
respectively):
FR3: N
N R N
N R N
N R N
N R
VR3: R
N N N
R R N
R N N
N N
If you examine these schedules, you will see that each has 4 R
trials, and 8 N trials. The ratio (or density) of reinforcement
is thus 4/(4+8) = 4/12 = 1/3. Or in other words, one out of three responses,
on average, works. (Note that on the next 12 trials, the FR schedule should
look exactly like the one above, but the VR schedule will be different,
since it follows no fixed pattern, but is assigned randomly, so long as
the right density is maintained.)
As was the case with FR schedules,
VR schedules with higher ratios (lower density of reinforcement)
will show greater resistance to extinction. And if we compare VR
and FR ratios to one another (where the ratio stays the same), then we
will generally find that a VR schedule gives greater resistance to extinction
than its corresponding FR schedule (though this is more likely at high
ratios).
Although it is a perhaps
macabre example, Russian Roulette qualifies as a variable ratio schedule.
So do lotteries and slot machines.
In a fixed interval schedule
(abbreviated FI), we establish a certain interval of time after
which the first response works in obtaining the reward. In particular,
responses during the interval are basically ignored by the experimenter:
They are completely ineffective. Thus, in a FI2 schedule (where we will
assume that the intervals are measured in minutes), the first response
after a 2-minute interval works, whether that response comes immediately
after the interval, or 5 hours later. An example of a fixed interval may
involve the times at which you feed your pets. If you always feed them
at the same times, then any response they make of going to the food area
before the right time is ineffectual. Similarly, many people get paychecks
on Friday afternoon, after they have put in a week's worth of work; going
to get your paycheck before the proper time will not be an effective response.
When does the next interval
start? In the feed-your-pets example, the interval in some sense depends
on how much time has passed. But normally, the intervals in these schedules
are started after a reinforced response. Thus, on that account,
an animal who doesn't respond until 5 hours after the end of the first
interval gets the reinforcement at that time, and simultaneously causes
the next interval to start counting down. These types of schedules are
useful ways of probing an ability to judge the passage of time.
As was the case with high
ratios, long intervals lead to better resistance to extinction.
So, an FI200 would be a better schedule to use than an FI3 if you want
the learning to last while at the same time you want not to rely too heavily
on always providing reinforcers. Again, you ought to be able to figure
out why the Discrimination Hypothesis would also make this particular
prediction. And as was true of the ratio schedules, high or long interval
schedules are often taught through a process of weaning the animal to longer
and longer waits.
Our final simple schedule
is the variable interval schedule (abbreviated VI). Much
as was the case for the variable ratio schedule, the variable interval
schedule involves presenting the animal with a series of intervals
in an unpredictable order. Within any such series, of course, we can determine
what the average interval might be. So, in an FI23 schedule, the
interval will always be 23 minutes, whereas in a VI23 schedule, the average
of the many different intervals will turn out to be 23. And as was the
case when we compared fixed and variable ratios, a comparison of fixed
and variable intervals will reveal that resistance to extinction will
be stronger in the VI schedules, all other things (such as the average
size of the interval) being equal.
As an example of a VI schedule,
imagine planning to buy something (a specific TV) at a store which is having
a closing sale. The sale will start at 5 to 10% off, and over the next
several weeks, will go to really spectacular savings such as 80% off. The
problem you face is knowing when to buy, since more and more merchandise
will disappear as the sale goes on. So, you can't wait a certain interval;
instead, you will have to constantly check on how much of what you want
is left as the prices get slashed, to try to get your best deal. That means
you will respond a lot. And that is basically what happens in this type
of schedule: a very high rate of response coupled with high resistance
to extinction.
Although these different
types of schedules do have different effects on performance, comparing
ratio to interval schedules can be a bit difficult. Nevertheless, we can
look at such things as response rate with these. Let us restrict ourselves
to variable schedules for the moment. With high ratios/intervals, one interesting
finding that occurs is that responses tend to come faster in a variable
ratio schedule than in a variable interval schedule. In a VR schedule using
pecking as a response in pigeons, it is not impossible to find rates of
over several hundred responses per minute! Such high rates are not
often found with VI schedules, however. Indeed, rates over 100 responses
per minute would qualify as high in VI.
Also, the response curves
tend to exhibit certain characteristics that seem to be schedule-specific
in the fixed schedules, so long as the ratios/intervals are high.
Thus, in the fixed ratio schedule, a very commonly reported finding involves
what is called a post-reinforcement pause: After a response that
works, there is a period of inactivity, and then the animal starts emitting
responses in a relatively high burst, and at a relatively constant rate
of speed. There will necessarily be some little pause in all schedules
while an animal consumes its reinforcement, of course; the post-RF pause
we are talking about here is an unusually long pause that extends well
past the time to eat or drink.
Let us go back to the feed-your-pets
example to see what happens in a fixed interval schedule. In this example,
you are not likely to have pets crowding underfoot as you move into the
food area, if it is not their time to be fed. But, the closer to feeding
time it is, the more likely it is that the animals will take an interest
in your presence in the feeding areas. My cats, for example, are very likely
to be underfoot (and a hazard to human locomotion!) when I go near their
feeding areas within 20 or so minutes before the time I normally feed them.
And that is basically also the pattern we find in the lab: Little or no
activity immediately following a reinforcement, and then a gradual rise
in activity as the interval winds down, with a very rapid burst of responses
right towards the end. Because of the changing rate at which the animal
responds, the impression one has in looking at the response rate following
reinforcement is of a curve. That characteristic is referred to as a scallop.
Figure 3 presents idealized response curves for the four schedules.
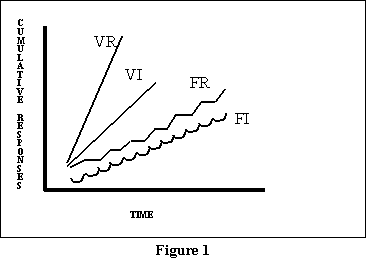 In this figure, as the lines slope higher and higher to the left, responding
is getting faster and faster (since there will be more responses per some
interval of time). That is why I have indicated a steeper line for VR (suggesting
fastest responding in that situation). But do note the difference between
the post-RF pauses in the FR schedule (the spots where the line goes flat),
and the scallops in the FI schedule. Close inspection of real data collected
using VR schedules will also occasionally show post-RF pauses, but these
are of much smaller magnitude, and so easily missed. Normally, if you see
a schedule with noticeable pauses or staircasing, it is a good bet that
you have an FR schedule.
In this figure, as the lines slope higher and higher to the left, responding
is getting faster and faster (since there will be more responses per some
interval of time). That is why I have indicated a steeper line for VR (suggesting
fastest responding in that situation). But do note the difference between
the post-RF pauses in the FR schedule (the spots where the line goes flat),
and the scallops in the FI schedule. Close inspection of real data collected
using VR schedules will also occasionally show post-RF pauses, but these
are of much smaller magnitude, and so easily missed. Normally, if you see
a schedule with noticeable pauses or staircasing, it is a good bet that
you have an FR schedule.
Other Schedules
Three other types of schedule
that may be briefly mentioned include chained, multiple, and concurrent
schedules. In chained schedules, two (or more) schedules run in
sequence, so that the animal has to perform according to the rules of both
before being able to make a reinforced response. As an example, an FR10-FI2
schedule would require the animal to make 10 responses, following which
a 2-minute interval starts. The tenth response meets the rule for the FR
schedule, but instead of providing a reinforcer, it activates the second
schedule (the FI schedule). So, it will be the first response that
occurs after this interval is up that gets the reinforcer. If the
animal only makes 9 responses, waits an hour, and then makes a tenth response,
that doesn't get any reinforcement because the interval did not yet start.
Conversely, in an FI2-FR10 schedule, a response made after the 2-minute
interval is up would initiate an FR10 schedule, so that another 10 responses
would be required before a reinforcer could occur. As you may imagine,
chained schedules allow us to test the sensitivity of the animal to complex
patterns.
You have already read about
one study using multiple schedules (and you will read about more
below). In these, the animal has several training sessions, each of which
may involve a different schedule. Thus, the experiment discussed above
by Dyal and Sytsma provided two groups who differed in whether they
had continuous reinforcement followed by partial reinforcement, or partial
reinforcement followed by continuous reinforcement. Multiple schedules
may be used to test sensitivity to changes in the animal's world, for example.
We can set up several sessions such that the world is becoming an increasingly
predictable place, or an increasingly unpredictable one (see the study
by Hulse at the end of this chapter).
And you have also read a
bit about concurrent schedules. In these, the animal may typically
choose any of several responses to make on a given trial (pressing the
blue lever or pressing the red lever, for example), but each response will
be associated with a different schedule of reinforcement! Herrnstein's
Matching Law, described in Chapter 4, involved concurrent VI schedules.
To remind you of what he found, animals tended to distribute their responses
in proportion to the 'goodness' (measured by amount, density, or delay
of reinforcement) of each: The response that led to the best outcome was
made most often; the one that led to the second-best outcome occurred second-most
often, and so on.
DRL & DRH Schedules
A final set of schedules
we will discuss include DRL and DRH schedules (standing,
respectively, for differential reinforcement of low rates of responding,
and differential reinforcement of high rates of responding). DRH
schedules involve reinforcing the animal for making rapid responses.
As you might imagine, such schedules are somewhat compatible with what
an animal would do anyway, since rapid responses normally result in obtaining
reinforcement sooner. Moreover, such rapid responding over a relatively
long period of time should lead to getting more reinforcements.
(Think of an animal on an FR30 schedule, for example, and allow it an hour
in a Skinner box. An animal making its 30 responses at a relatively slow
rate of speed will accumulate less rewards than an animal making its 30
responses at a relatively high rate.) Still, we can ask an animal to respond
at a rate normally higher than it would, left on its own, and in such a
case, we have a DRH schedule.
Much more interesting are
the DRL schedules (see, for example, the review article by Kramer and Rilling).
In these, we reinforce the animal for waiting a certain amount of time
between its responses. Specifically, an animal that responds too soon
not only fails to get a reinforcer, but also resets the interval so that
it now has to wait even longer between reinforcements. (If the interval
we set is 20 sec, for example, an animal responding at 18 sec after the
last reinforcer will reset the interval so that it must wait an additional
20 sec before responding: a total of 38 sec since the last reinforcer).
Such schedules should remind
you of the work we discussed earlier on omission training. As was
true of omission training, DRL schedules are initially more difficult to
acquire. They also tap into an animal's sensitivity to time. And as the
interval in the schedule increases, the schedule becomes harder and harder
to acquire. In DRL, the animal will typically make a number of non-reinforced
responses (which is why this particular schedule qualifies as a partial
reinforcement schedule, in case you were wondering!). Thus, in part because
of these and because of the conditioning of waiting, a partial reinforcement
effect is predictable.
One more feature of DRL is
of interest: Many of the animals during the waiting period do not
wait passively. Instead, they engage in other types of stereotyped
behaviors. This might remind you a bit of Skinner's discussion of
superstitious behavior presented in Chapter 4, but it is really
not the same thing: These responses occur well before the reinforcement
(i.e., weak temporal contiguity, at best), which in any case is due to
the final response that is not superstitious. Several theorists have speculated
that these behaviors are ways in which an animal can time an interval.
In this sense, they correspond a bit to our talking to ourselves ("one-thousand-one,
one-thousand-two") as a way of estimating passage of time.
With this as background,
let us go on to consider the two most cited theories of the PREE. As we
do, you may wish to consider how each might predict the findings with these
various schedules.
C. Two Theories Of Partial Reinforcement
The two major theories of partial
reinforcement are Amsel's Frustration Hypothesis, and the Sequential
Hypothesis of Capaldi. Each has its strengths and its weaknesses.
They are also similar in certain respects. As you will see, each relies
on a mechanism of classical conditioning to account for some of
the resistance that occurs in partially reinforced animals, and each contains
a component of discriminability. Let us start with Amsel.
Amsel's Frustration Hypothesis
The basic insight behind
Amsel's theory is that an expectancy of reinforcement can cause frustration
when it is not fulfilled. Failure to obtain an expected reward is an
unpleasant experience. Amsel focuses on the consequences of frustration
in accounting for partial reinforcement effects.
One of the major concepts
in the theory is that of the primary frustration response, RF.
The primary frustration response is the response that occurs on failure
of reinforcement. Just as was true of the primary goal response
we talked about in an earlier chapter (Chapter 4), the primary frustration
response can be thought of as including a number of components, or fractions.
These are presented in analogous fashion to the fractional goal responses;
that is, they are conceived of as rf...sf
units in which frustration has both the qualities of a response to a situation,
and concomitant internal stimulation. As you might guess from the description
so far, these rf...sf components can become
mediators that become conditioned to various stimuli and responses
in a situation. Thus, when an animal becomes frustrated in the presence
of some stimulus S (or while doing some response R), various frustration
mediators (biting, for example; or more generally, the tense feelings associated
with frustration) may become associated with the S and the R. One thing
about these that is critical for you to notice is this: There will be
few or no such rf...sf mediators during acquisition
for animals that are continuously reinforced, as they do not experience
frustration. In contrast, animals that undergo partial reinforcement
will have many of these rf...sf mediators
present in their environments during learning.
With this as background,
we can now include three effects will characterize frustration, and that
will depend on the presence of these mediators. In homage to the theories
of extinction we looked at in an earlier section, these three effects are
drive, discriminability, and response competition.
Specifically, according to Amsel, frustration is an unpleasant drive that
can motivate animals to avoid what has been frustrating them (due
to the negative reinforcement of a decrease in frustration). At
the same time, because it is a drive, it increases the overall activity
level of the animal, which can eventuate in new responses, and thus, the
possibility of learning competing responses to those that led to
the frustration. And finally, the similarity of frustration experiences
during learning and extinction can determine how much generalization there
is between these two situations. Thus, the more different the frustration
cues are in the two situations, the easier it will be to learn a new response
during extinction (similar to what Mowrer and Jones claimed). Accordingly,
Amsel's theory borrows a little bit from all the previous theories we've
looked at, and by doing so, avoids problems that any single theory might
have had.
Let's first briefly look
at evidence relevant to the drive and competing response effects of frustration,
and then we'll talk about how the model plays its predictions out in continuous
and partial reinforcement.
In one famous experiment,
Daly experimentally frustrated one group of rats by not feeding
them in a spot where they had normally been fed before (similar to the
procedure used by Seward and Levy). She then allowed these rats
to learn a response that would get them away from this spot. There was
no other reinforcer for learning this response other than escape from frustration.
Nevertheless, the animals did acquire the response. Her argument was thus
that getting away from some place where you've been frustrated is rewarding.
This constitutes a claim that reduction in frustration acts as a negative
reinforcer. You can now see how some such mechanism as this can account
for the Seward and Levy findings on latent extinction.
Another claim associated
with the concept of drive is that increasing drive level ought to increase
the overall activity level. That claim was in part examined by Amsel
and Roussel. They trained rats to run to a goal box using continuous
reinforcement for the first 80 or so trials. Following that, they switched
to reinforcing only half of the trials. Following a non-reinforced trial,
they observed faster running, consistent with a claim that these animals
were aroused and energized. In a variant of this procedure, a dual-goal
box alleyway was used in which the rats ran to goal box 1, and then after
a short stay, were allowed to go through a door into an alley leading to
goal box 2. These animals were always reinforced at the second goal box,
but received reinforcements only half of the time at the first goal box.
If they were not fed at the first stage, then (as in the first experiment),
they ran faster to the second stage.
Finally, what about competing
responses? Energized behavior ought to result in the possibility of other
behaviors being expressed. One of the observations a number of people have
made (including Mowrer and Jones) is that frustrated animals engage
in a much higher level of aggressive behavior. So, you can see from this
the possibility of learning some sort of response that competes with the
original because it involves getting rid of the frustration.
Now that we've looked at
some of the properties of frustration, let's discuss its effects on continuously
reinforced responding. Here, the important point to note is that frustration
will not be present during learning. The first point at which real frustration
arises is when the animal hits the extinction phase. Hence, a frustration
drive arises at extinction that can cause competing responses, and that
opens up the possibility for negative reinforcement when the animal stops
doing whatever it is that leads to frustration. At the same time, the presence
of frustration cues during extinction (the rf...sf
mediators) makes extinction a very different world or stimulus complex
than learning. So, for all of these reasons, extinction following continuous
reinforcement ought to be relatively quick.
But can we say anything further
than this? Fortunately, we can. Basically, Amsel has predicted that the
bigger the difference there is in frustration between learning and extinction,
the faster extinction ought to occur. (Note that this prediction specifically
applies to the continuous reinforcement situation!) This should make sense
to you on all three components of the theory: (1) Bigger frustration means
more negative reinforcement, resulting in stronger learning; (2) bigger
frustration means higher levels of arousal, resulting in more alternative
behaviors from which competing responses may be acquired; and (3) bigger
frustration means a greater discriminability between learning and acquisition,
which should result in faster learning of a new response to the extinction
situation. As you know from our discussion of results like Roberts's,
animals that receive large reinforcers during learning show faster extinction.
Losing a large reinforcer, of course, is more frustrating than losing a
small reinforcer, so this finding fits in with the predictions.
But what of partially reinforced
animals? The important point here is that frustration cues (the rf...sf
mediators) are present during acquisition. Because these cues are present,
and on a number of trials become followed by reinforcement, they become
classically conditioned cues for reinforcement. That is, the reinforcer
is the UCS, while the frustration (the rf...sf
mediators) is the CS. So, the animal learns that feeling frustrated is
a cue or predictor for being fed, since feeling frustrated in the past
has been followed by food. Put simply, we not only train animals to tolerate
frustration, we also train them to reinterpret its significance:
Instead of being a negative event, frustration becomes a signal for a positive
event (the reinforcer).
And of course, the higher
the frustration the animal is exposed to during learning, the more similar
learning will be to extinction (in which there is a very high level of
frustration, indeed!). Thus, the second part of the prediction Amsel makes
(confirmed by Roberts) is that partially reinforced animals ought
to show a reverse reinforcement-size effect: Animals trained with
large reinforcers should show greater resistance to extinction.
Indeed, we can make this prediction for two very different reasons. One
involves the afore-mentioned issue of discriminability: With larger reinforcers,
there is a higher level of frustration on non-reinforced acquisition
trials, making these more like extinction. But the second is that large
reinforcers also act as more intense UCSs that result in better
conditioning of the CS (the rf...sf mediators).
In terms of drive level,
then, high frustration during learning is 'good' and results in greater
generalization, and more vigorous responding during learning (which will
persist into extinction). At the same time, since the responding eventually
succeeds in obtaining a reinforcer in the acquisition phase, competing
responses are not acquired; the additional energization caused by frustration
gets channeled into the learned response. And finally, of course, there
are obvious implications for discriminability. Indeed, you can see that
high ratios or intervals in partial reinforcement schedules should result
in more frustration than low ratios or intervals. And intuitively, you
should see that high ratios or intervals involve less discriminability
because extinction can be defined as a very long sequence of time without
reinforcement (which is what happens in high ratio/interval) schedules.
The theory thus has the merit of being able to explain a number of effects
with a few well-argued principles. Its claims regarding the opposite effects
of reinforcement size in partial and continuous reinforcement are regarded
as among its strongest successes.
Capaldi's Sequential Hypothesis
An alternative approach has
been championed by Capaldi. In his work, the stress will be on memory of
events (as it was in the Wagner model of classical conditioning).
As in Amsel's theory, there will be conditioning of cues that predict a
reinforcer; and as in Amsel, there will also be a question of how similar
these cues are in the learning and extinction environments. But, there
is no specific mention of frustration as a mechanism in Capaldi's theory,
and indeed, he has published some experiments claiming to find evidence
against that mechanism. Rather, the focus is on non-reinforced trials.
His basic idea has to do with how salient these become in an animal's memory.
The longer the period of non-reinforcement during learning, the more salient
these are.
Several people have done
studies attempting to determine how many pairings of a response and a reinforcer
it takes in order to develop an expectancy of reinforcement: an ability
to anticipate that a reward will follow the execution of a response. One
way in which to do so is to adopt Amsel's claim that failed expectancies
lead to frustration, and that frustration energizes behavior. In studies
such as these, the question is, how many pairings do we need before we
see that a non-reinforced trial changes the animal's behavior? In one such
study, Hug claimed that at least 8 or so pairings
were required.
If that number is correct,
then there are several studies demonstrating a partial reinforcement effect
before expectancies have developed! One such study is by Godbout,
Ziff, and Capaldi. They took several groups of animals and provided
them with very small numbers of response-reinforcer pairings. In fact,
these varied between two and five pairings (well below the minimum number
that Hug claimed was necessary for frustration). Of course, we can include
non-reinforced trials among these for some of our groups in order to assess
a partial reinforcement effect. In any case, following this very brief
acquisition period, we start the animals on extinction. Compared to animals
that received only continuous reinforcement, the animals with partial reinforcement
extinguished more slowly. And the point here, of course, is that if these
animals had not developed frustration, then there should have been no opportunity
to condition rf...sf cues, and thus, no way
in which extinction and learning would have differed (in terms of discriminability)
for the partially reinforced and continuously reinforced groups.
Another study by Capaldi
and Waters is even more interesting and suggestive. In this study,
rats ran down an alleyway for a reinforcer. Capaldi and Waters provided
slightly different acquisition experiences for three groups of rats, before
putting them all through extinction. Their design was basically the following:
Group Phase 1
Phase 2
1
5 continuously reinforced (CRF) trials
extinction
2
10 continuously reinforced trials
extinction
3
5 non-RF trials followed by 5 CRF
extinction
The question they asked was
whether the groups would all extinguish at the same rate. Note that Hug's
work might suggest fastest extinction for Group 2, because that
group has perhaps enough trials to develop an expectancy, resulting
in frustration during Phase 2. However, the frustration hypothesis would
seem to predict that Groups 1 and 3 should extinguish at the same rate.
Both have had 5 continuously reinforced trials, and if Hug's conclusions
are correct, neither should have developed the frustration mechanism. But
suppose Hug is wrong, and animals can build up an expectancy in fewer than
8 trials, though perhaps not one strong enough to manifest itself in overtly
energized behavior. Even if Hug's conclusions are wrong, Groups 1 and
3 should still extinguish at the same rate, because Group 3 should
effectively act like a continuously reinforced group! The reason is
that Group 3 starts out with non-reinforcement. Since they have
had no previous experience of reinforcement, non-reinforcement in the
first 5 trials cannot cause any frustration! Their expectancy starts
to form on Trials 6 through 10, and that involves the same number of pairings
(and therefore the same learning of an expectancy) as Group 1. Thus, the
predictions that Amsel's theory could make in this experiment seem quite
clear.
As you may have guessed,
Group 3 showed a partial reinforcement effect. It can't have been due to
frustration and the rf...sf mechanism. It
must therefore have been due to something else. That something else is
what Capaldi's theory seeks to address.
So what is it that is important
about Group 3, and that can result in a PREE? According to Capaldi, the
answer is that Group 3 had a sequence of non-reinforced trials that
was terminated by a reinforced trial. His theory is called the sequential
hypothesis because it is the sequence of non-reinforced trials that
will prove critical.
The theory is memory-based,
as indicated above. The idea here is fairly simple. What happens after
a trial becomes part of the animal's memory (specifically, its short-term
or working memory, as in Wagner's model). Those memory traces
will still be present when the animal undergoes the next trial. If there
is a reinforcer on the next trial, then the memory traces get conditioned
to the reinforcer. In this case, the reinforcer acts as the UCS, and
the memory traces constitute the CS. Thus, the memory traces, through
classical conditioning, come to predict the reinforcer.
In extinction, the memory
traces will include whatever experiences are associated with not
being reinforced. Hence, to the extent that similar traces were conditioned
during acquisition, learning and extinction will be similar: The animal
in extinction will experience cues that keep 'promising' a reinforcer,
thus motivating its continued responding. With that as an overview, let's
focus on the specifics.
We will start with a simplifying
assumption that the animal's memory cues include being reinforced on previous
trials, or not being reinforced on previous trials. We will, moreover,
assume that the animal has one or the other of these states, but
not both (but see the next section below for some contrary evidence!).
The longer the animal has been in a particular state, the more salient
that state is. Thus, an animal that has not been fed on the previous ten
trials has a relatively salient or strong memory of non-reinforcement compared
to an animal that has not been fed on a previous three trials. And of course,
whatever state of memory the animal is in ceases the moment the
opposite event occurs. So, an animal that is in the reinforcement state
enters the non-reinforcement state when it hits a non-reinforced trial,
and conversely, an animal in the non-reinforcement state enters the reinforcement
state with its first reinforced trial. A very simple way of thinking about
this is that an animal's working memory acts like a two-state toggle switch:
Reinforcement toggles its working memory into the reinforcement state,
and non-reinforcement toggles its working memory into the non-reinforcement
state (much as a light switch being pushed up or down toggles the light
on or off).
Let us call the memory of non-reinforcement an N-memory
(abbreviated MN), and the memory of reinforcement an
R-memory (abbreviated MR). We can now indicate
the salience or intensity of this state by adding a number that indicates
approximately how long the animal has experienced the state. Since this
number will be a function of how many past trials of reinforcement or non-reinforcement
the animal has had, we can use the number of identical trials as a rough
indicator of salience. Accordingly, an animal that has just finished its
third non-reinforced trial will be in the MN3 state, whereas
an animal that has just finished its tenth reinforced trial will be in
the MR10 state. (We do not have to assume that animals can do
anything like counting; the numbers here do not imply that! Rather, the
idea is that there is some qualitative sense of how long an animal has
been in a state, perhaps due to the state getting stronger with each additional
repetition of a given event. Even though counting is not an issue here,
however, you may enjoy looking at an article by Capaldi and Miller
that claims rats can count!)
One more concept needs to
be added, although we have been talking about it implicitly. It is the
notion of an N-length. An N-length is the run or number of non-reinforced
trials in a row. The N-length, of course, determines the salience of
the N-memory: As the N-length increases, the MN state strengthens.
In the Capaldi and Waters experiment presented above, for example, the
N-length for Group 3 was 5, so that on the 6th trial, the animals
should have been in the MN5 state.
Given this, the point that
will be important is that when an N-length is followed by a reinforcer
(causing the non-reinforcement state to toggle to reinforcement), there
will be conditioning of the MN that was in the animal's
working memory. This is because the MN serves as the CS
that is present when the UCS (the reinforcer) occurs. Thus, in Capaldi's
theory, increased resistance to extinction in partially reinforced animals
arises in part because the animal learns that the MN state predicts
upcoming reinforcement. And of course, the more similar the MN
state during learning is to the MN state the animal experiences
in extinction, the longer the animal will respond.
Let's work through an example,
in order to see this better. We will take animals that are repeatedly exposed
to the same pattern, and we will assume that they have had prior training
with this pattern, so that we are looking at trials in the middle of their
acquisition. Let us assume the following pattern of reinforced and non-reinforced
trials (using R and N for reinforced and non-reinforced trials,
respectively):
Trial: R
R N
N R
R R
N N
N R
What ought to be in the animal's working memory on each of these trials
may now be indicated as follows:
Trial: R
R N
N R
R R
N N
N R
Memory: MR1
MR2 MR3 MN1
MN2 MR1 MR2
MR3 MN1 MN2
MN3
Here, the first MR1
occurs because the trial prior to the first trial above was an R-trial
(recall that this pattern is constantly recycling, so look to its end to
see what came immediately before!). But now, let us also ask what types
of classical conditioning of memories occur. In order for there to be classical
conditioning on a given trial, there has to be a reinforcer (an R).
Essentially, two types of memory states are being conditioned here. On
some trials, the animal has reinforcement cues from the previous trial
when a reinforcement occurs (resulting in conditioning of the MR
state), and on other trials, the animal has non-reinforcement cues (involving
conditioning of the MN state). Using plus signs to indicate
trials on which such conditioning occurs, we now obtain the following diagram:
Trial: R
R N
N R
R R
N N
N R
Memory:
MR1 MR2 MR3
MN1 MN2 MR1
MR2 MR3
MN1 MN2 MN3
MR Learned: ++
++
++ ++
MN Learned:
++
++
As you can see from this
example, in this particular sequence of trials, there are four occasions
on which a memory of reinforcement is paired with a UCS, and two occasions
on which a memory of non-reinforcement is paired with a UCS. The pairing
of a UCS with a memory of being reinforced is not terribly noteworthy for
our discussion of extinction, because reinforcement cues by definition
will not be present in extinction. So, we need not discuss that particular
type of association any further. But the pairing of a UCS with the memory
of non-reinforcement is quite another matter: Those two trials are where
we train our animal to tolerate non-reinforcement similar to what it will
experience in extinction.
There are a number of principles
we can derive from this approach, but here are three. The first (the
Principle of N-length) is that resistance to extinction ought to
increase as the N-length increases. The reason is that longer N-lengths
mean longer MN, which are more similar to the excessively long
MN the animal will experience in extinction. And indeed, Gonzalez
and Bitterman, for example, have obtained this result. But then, you
knew about that anyway, since we already discussed the finding when we
talked about how increasing ratios and intervals led to greater resistance
to extinction. In an FR200 schedule, for example, the N-length will be
199, compared to a N-length of 9 in an FR10 schedule.
The second principle (the
Principle of Transitions) is that resistance to extinction ought
to increase with the number of transitions from N to R. A transition
is the trial on which the N-length stops because a reinforcement has occurred.
On this definition, wherever there is a transition, there will be a conditioning
trial (involving pairing of MN with a UCS). Thus, number of
transitions corresponds directly to the number of times a CS and a UCS
have been paired.
The third principle (the
Principle of Variability) is that resistance to extinction ought
to increase as a function of the number of different N-lengths encountered.
This principle doesn't refer to how many N-lengths the animal experiences
(Principle 2 does that!), but rather how many different types of
lengths the animal experiences. In our example above, there were two types
of N-lengths: a length of 2 (resulting in MN2) and a length
of 3 (resulting in MN3). Because that was a recurring pattern,
the animal only ever experiences two different types of N-lengths until
it hits extinction. On the other hand, it will have many, many transitions,
and not just the two that appeared above. If the sequence above
were repeated 200 times during learning, for example, then the animal will
have experienced 400 transitions (since there are two transitions
per sequence), but still only two different types of N-lengths.
The Principle of Variability
may be thought of as a principle of predictability. The more different
types of N-lengths the animal has been conditioned to, the less certain
it can be that the N-length experienced during extinction is different
from what happened during learning. As in Amsel's theory, animals repeatedly
trained to the same N-length may develop an expectancy of about when the
N-length should terminate. Such an expectancy could help them discriminate
between learning and extinction. Varying the N-length prevents that. And
you also already know the evidence supporting this principle: Variable
reinforcement schedules do indeed lead to greater resistance to extinction
than fixed schedules, all other things being equal.
So, to go back to the Capaldi
and Waters (and Godbout et al.) studies, a PREE with very few trials is
possible so long as there is a transition. In Capaldi and Waters's
Group 3, for example, there was indeed one transition involving conditioning
of an N-state.
These aren't the only principles
that govern what should happen here. Just like Amsel, Capaldi can also
account for the reinforcement size effect. Thus, on a transition, a larger
reinforcer means a stronger UCS, which means stronger learning. And of
course, during continuously reinforced learning, animals never become conditioned
to N-lengths, accounting for why these will extinguish relatively rapidly.
Similarly, reinstating learning cues during extinction ought to slow extinction,
whereas changing such cues ought to speed it up. You already know several
studies that support that particular claim. Finally, disrupting the animal's
memory prior to a transition ought to influence the success of conditioning,
because it ought to change the N-memory.
As a final example of work
compatible with Capaldi's theory, we will examine a finding by Capaldi,
Hart, and Stanley. In involves what is called ITR (intertrial
reinforcement). In ITR, animals are given a reinforcement between
trials that has nothing to do with a response, or indeed, with
being in the experimental apparatus. To see what might happen, let us set
up a number of groups. We will, again, assume that all groups are somewhere
in the middle of their learning, and are receiving the same sequence (presented
below) over and over again. We will use I
for the ITR. Here is the sequence:
Group
Repeating Acquisition Sequence
1
R
N
N
N
R
2
R
N I
N
N
R
3
R
N
N I
N
R
4
R
N
N
N I
R
The question is, what will
happen when all of these groups are put through extinction? To see, let's
add in the N-states:
Group
Repeating Acquisition Sequence
1
R
N
N
N
R
MR1
MR2
MN1
MN2
MN3
2
R
N I
N
N
R
MR1
MR2 MN1 MR1
MN1
MN2
3
R
N
N I
N
R
MR1
MR2
MN1 MN2 MR1
MN1
4
R
N
N
N I
R
MR1
MR2
MN1
MN2 MN3 MR1
Notice what happens. The
ITR In Groups 2 and 3 chops up the N-length, because it toggles the state
in the animal's working memory. Also, in each group, the ITR is
associated with an N-length, so there should be some conditioning
of the N-length to it (since it is a UCS, by definition). But
whatever conditioning occurs to the ITR is completely irrelevant to extinction.
The reason is that the animal is no longer in its apparatus, so that it
is learning that when it has an N-state and it is in the spot where
it has received ITR, expect a reinforcer. But when it is back in the apparatus,
the environmental cues associated with where it received an ITR have been
toggled to the experimental context cues, so that that particular expectancy
is no longer in operation. Thus, the additional transitions and N-length
variability caused by ITR do not influence what happens in the learning
(and therefore, extinction) context. So, we need look just at where
a transition occurs in the learning environment. For Groups 1 through 3,
that transition occurs on the last trial. And as you can see from the table
above, the N-state that gets conditioned on the last trial becomes smaller
and smaller. By the Principle of N-length, then, we would expect less and
less resistance. Capaldi et al. do indeed find that ITR inserted into an
N-length reduces the resistance to extinction, as our discussion of the
example above would suggest.
What about Group 4? Rather
surprisingly, the analysis above suggests that Group 4 ought to act in
some sense like a continuously reinforced group! The reason is that the
placement of ITR in Group 4 has prevented the conditioning of any N-state
within the experimental context. That, in turn, suggests that partial reinforcement
schedules may sometimes give results identical to continuous reinforcement
schedules (or at least, fail to yield the usual PREE). We will see below
some further evidence questioning whether greater resistance to extinction
is always found with partial reinforcement.
Although Capaldi's theory
does an excellent job of handling a number of findings, it too, like Amsel's
theory, has its problems. One such problem occurs in a study conducted
by Hill and Spear. They put their animals through extinction under
a fairly unusual set-up; namely, they ran one extinction trial
per day. Since the contents of working memory do not last the
whole day, this means that the animals during extinction ought always to
have experienced a minimal N-state (namely, MN1). Under
these circumstances, animals conditioned with higher ratios ought
to have more discriminability with the extinction conditions, and
not less (MN200 is more different from MN1 than MN2
is, for example). Thus, animals with higher ratios ought to have faster
extinction, in contrast to the usual partial reinforcement findings. This
prediction of Capaldi's, however, proved false. (And note that this study
poses problems for Amsel, as well!)
A second series of studies
that also seems incompatible with Capaldi was done by Pavlik and
colleagues (e.g., Pavlik and Carlton). They used concurrent schedules,
except that instead of the two stimuli being present simultaneously, only
one was present on a given trial. Each stimulus, of course, was trained
with a different schedule. One of the schedules involved continuous
reinforcement, and the other involved partial reinforcement. Thus, unlike
the vast majority of studies in which different groups of animals
experiencing different schedules were compared, these studies involved
the same animals experiencing both types of schedules. And
when that happens, the response on the continuous reinforcement schedule
takes longer to extinguish. That is a curious finding, and it is hard to
know what to make of it. I suspect that its ultimate explanation may turn
out to involve components of a contrast effect. But in any case, since
there were no N-lengths or frustration conditioned to the stimulus on the
continuously reinforced schedule, neither Capaldi's nor Amsel's theory
would elegantly handle this finding.
III. Complex Pattern Sensitivity
One of the fascinating areas
of research relevant to resistance to extinction concerns animals' sensitivity
to complex patterns of reinforced and non-reinforced trials. Let's start
with a sample study by Hulse that involves using multiple schedules of
reinforcement. In this study, Hulse used four groups of rats. Each had
three successive schedules of reinforcement during acquisition, followed
by a final phase of extinction. The schedules involved a random partial
schedule (Random), a systematic partial schedule involving a repeating
pattern (Systematic), and a continuously reinforced schedule (Continuous).
The design was as follows:
Group
Phase 1
Phase 2
Phase 3
Phase 4
1
Continuous Continuous
Continuous
Extinction
2
Random
Random
Random
Extinction
3
Continuous Systematic
Random
Extinction
4
Random
Systematic Continuous
Extinction
Of course, predicting what
should happen in the first two groups is easy: There should be a partial
reinforcement effect. The interesting question is what to expect in the
last two groups. There are a number of possibilities here, depending on
which set of theories you wish to apply. Using the Mowrer and Jones
Discrimination Theory, and based on the results of the study by
Dyal and Sytsma, for example, we might predict that Group 3 will be
equal to Group 2, and that Group 4 will be equal to Group 1. This prediction
is based on claiming that only what the animal has learned in the last
phase before extinction is relevant. So, Groups 2 and 3 should have
the same relatively low discriminability between Phase 3 and extinction,
whereas the other groups should have the same relatively high discriminability.
Alternatively, both Amsel's
and Capaldi's theories may be used to predict that Groups 3 and 4 should
be equal to one another. Each has had the same experiences, only
in different order. On this account, each should have had the same number
of conditioning trials involving frustration cues (rf...sf)
or N-states (MN) predicting reinforcement. Moreover, since
there have been more of these trials in Group 2 than in Groups 3 and 4
(Groups 3 and 4 have one phase in which there is no such conditioning
due to continuous reinforcement!), we may also predict that resistance
to extinction in Groups 3 and 4 will be more than Group 1's resistance,
but less than Group 4's.
Now that we have our predictions,
we can look at the results to see which of these two approaches is better
supported. And the answer turns out to be that neither one is correct!
It is certainly true that Group 3 has a very high resistance to extinction,
much as does Group 2. But the surprise is that Group 4 shows the most
rapid extinction. Even though they had two phases involving partial
reinforcement, they show less resistance than a continuously reinforced
group.
What is going on, here? In
fact, Hulse's finding fits in quite well with a type of cognitive expectancy
theory of extinction. But instead of the type of expectancy found,
say, in Amsel's theory (in which the animal is sensitive to what ought
to happen on a given trial), the expectancy here is a dynamic
one involving sensitivity to change and its consequences. If you go back
and look at Groups 1 and 2, you will see that their experiences never change.
The picture is very different for Groups 3 and 4, however. Group 3's world
is becoming less and less predictable over time, since it is moving from
continuous (perfectly predictable) to random reinforcement. In terms of
metalearning (learning about learning), Group 3 should thus be learning
to rely less and less on trying to predict or expect reinforcement. But
such metalearning is precisely the type of result that should yield
very high resistance during extinction. In cognitive expectancy theory,
of course, animals need to acquire a new expectancy about extinction. That
acquisition is triggered by evidence that the old expectancies are no longer
valid. But in Group 3, an animal that isn't relying on making predictions
won't be sensitive to when a prediction fails to come true, making the
acquisition of a new expectancy difficult. (This may remind you a bit of
what we talked about with respect to learned irrelevance or learned
indolence).
In similar fashion, Group
4's world is getting more and more predictable, going from complete unpredictability
to complete predictability. They ought to be learning that the outcome
of each trial increasingly can be taken to predict the outcome of the next
trial. Thus, when they hit extinction, assuming a strongly predictable
world, a non-reinforcement trial for them ought now to signal that the
next trial will be a non-reinforcement trial, as well. Thus, we would expect
them to show strong sensitivity to the change that occurs in extinction,
resulting in extraordinarily fast adaptation. Being able to predict changing,
evolving patterns in the world is a much more adaptive and useful skill
than simply developing an expectancy of what should happen on Trial
x based on the average of what has happened on all previous trials.
The world changes; and organisms that are sensitive to such changes will
be better situated to survive.
A follow-up study by Fountain
and Hulse demonstrates the same mechanism. They had rats run an alleyway
for reinforcers. In an initial learning phase, all animals were given sequences
of four trials in which each trial involved a different amount of reinforcement.
There were considerable breaks between these sequences. Then, in a test
phase, the rats were given a sequence of five rather than four trials,
but on the fifth trial, there was no reinforcement. Three groups
had the following setup:
Group Acquisition
Sequence
Test Sequence
1
14 7 3
1
14 7 3
1 0
2
14 5 5
1
14 5 5
1 0
3
14 3 7
1
14 3 7
1 0
As you can see, the first
group had a very simple pattern in which the amount of reinforcement decreased
steadily on every trial. In contrast, the other two groups also had patterns
that ended with the smallest reinforcement, but their patterns were not
as simple. Fountain and Hulse argued that if the rats were capable of learning
a rule specifying the pattern, then Group 1 should do best, since
theirs was the simplest rule (things are always decreasing from first
to last trial). Consistent with this claim, Group 1 on their test sequence
slowed their running considerably on the fifth trial, but the other two
groups did not.
This study is based on a
claim that rats are capable of learning rules for how things are organized.
That isn't the only theory that has been proposed to account for serial
pattern learning. Capaldi, Verry, and Davison, for example, have
claimed that serial pattern learning represents association learning
in which the previous trial acts as the stimulus cue for the next
trial. But that explanation cannot handle Fountain and Hulse's results,
because the animals in the test sequence had never been exposed to a 0-reinforcer
trial, and so could not have learned that a trial in which there was one
reinforcer was the stimulus cue for a trial in which there were no reinforcers.
In another, earlier experiment
by Hulse, rats were trained on a five-trial pattern that involved
either a simple or a complex rule. You can derive the rules by consulting
the design below:
Group
Acquisition Sequence
1
14 7 3
1 0
2
14 1 3
7 0
In this case, an association
learning model might predict that the fourth trial and the number of reinforcements
the rat obtains on that trial become a predictor for the fifth 0-reinforcement
trial. But if that is the case, then both groups ought to learn at about
the same rate. A rule-based model, on the other hand, would predict that
the simpler rule is more likely to be learned, so that Group 1 should show
enhanced performance. Consistent with that latter model, Hulse found that
the rats in the first group slowed down their running on the fifth trial
more than the rats in the second group. Both indeed learned that the last
trial in the sequence provided no reinforcement (as evidenced by the change
in their running speeds), but the learning was more successful in the first
group. And lest you think the results might have been due to the relative
similarity of reinforcement amounts in the fourth and fifth trials, be
advised that follow-up studies by Hulse and Dorsky repeated this
experiment, but with the complex and simple patterns having the same reinforcement
amount on the fourth trial (1 pellet).
In general, animals are sensitive
to changes. As reinforcement systematically increases across a repeating
sequence of trials, so do their responses. Contrarily, as reinforcement
systematically decreases, responses such as running slow down.
A number of people now study
animal sensitivity to patterns and sequences, in order to determine the
types of rules animals can acquire. Some of this involves very sophisticated
patterning such as birds' sensitivity to rhythm and pitch patterns (e.g.,
Hulse, Cynix, and Humpal). A good place to start, if you are interested
in this work, is the section on Sequence Memory in the Roitblat,
Bever, and Terrace volume on Animal Cognition. The notion of rule-based
learning strongly suggests that there may be more going on in extinction
than is suggested by models such as Amsel's or Capaldi's that focus on
the (classical) conditioning that occurs on an individual trial. They also
suggest an involvement of long-term memory (typically referred to as reference
memory in animals) in addition to working memory. The sequences animals
learn in some serial pattern experiments seem to extend well beyond the
limits of working memory. They would thus appear to require an ability
to compare what is going on now with what has gone on in the past.
A final point deserves mention
before we close out this chapter. In the real world, not every action results
in a successful outcome. So, a learning mechanism that allows persistence
in the face of non-reinforcement makes a lot of sense (see also Flaherty).
The partial reinforcement effect may thus be seen as the outcome of an
adaptive process. At the same time, the ability to acquire rules that are
sensitive to change is also extraordinarily useful and adaptive. What happens
with partial reinforcement may well depend on whether the situation calls
for associational or rule based learning. It is in part the difference
between static and dynamic expectancies.
Partial Bibliography
Adelman, H.M., & Maatsch, J.L. (1955). Resistance to extinction
as a function of the type of response elicited by frustration. Journal
of Experimental Psychology, 50, 61-65.
Amsel, A. (1958). The role of frustrative nonreward in noncontinuous
reward situations. Psychological Bulletin, 55, 102-119.
Amsel, A. (1962). Frustrative nonreward in partial reinforcement and
discrimination learning: Some recent history and a theoretical extension.
Psychological Review, 69, 306-328.
Amsel, A. (1992). Frustration theory: An analysis of dispositional learning
and memory. NY: Cambridge U. Press.
Amsel, A., & Roussel, J. (1952). Motivational properties of frustration:
Effect on a running response of the addition of frustration to the motivational
complex. Journal of Experimental Psychology, 43, 363-368.
Baum, M. (1970). Extinction of avoidance responding through response
prevention (flooding). Psychological Bulletin, 74, 276-284.
Boe, E.E., & Church, R.M. (1967). Permanent effects of punishment
during extinction. Journal of Comparative and Physiological Psychology,
63, 486-492.
Capaldi, E.J. (1967). A sequential hypothesis of instrumental learning.
In K.W. Spence & J.T. Spence (Eds.), The psychology of learning
and motivation, Volume 1 (67-156). NY: Academic.
Capaldi, E.J. (1971). Memory and learning: A sequential viewpoint. In
W.K. Honig & P.H.R. James (Eds.), Animal memory (111-154). NY:
Academic.
Capaldi, E.J., Hart, D., & Stanley, L.R. (1963). Effect of intertrial
reinforcement on the aftereffects of nonreinforcement and resistance to
extinction. Journal of Experimental Psychology, 65, 70-74.
Capaldi, E.J., Lanier, A.T., & Godbout, A.C. (1968). Reward schedule
effects following severely limited acquisition training. Journal of
Experimental Psychology, 78, 521-524.
Capaldi, E.J., & Miller, D.J. (1988). Counting in rats: Its functional
significance and the independent cognitive processes which comprise it.
Journal of Experimental Psychology: Animal Behavior Processes, 14,
3-17.
Capaldi, E.J., Verry, D.R., & Davison, T.L. (1980). Memory, serial
anticipation learning and transfer in rats. Animal Learning & Behavior,
8, 575-585.
Capaldi, E.J., & Waters, R.W. (1970). Conditioning and nonconditioning
interpretations of small-trial phenomena. Journal of Experimental Psychology,
84, 518-522.
Daly, H.B. (1970). Combined effects of fear and frustration on acquisition
of a hurdle-jump response. Journal of Experimental Psychology, 83,
89-93.
Dragoi, V., & Staddon, J.E.R. (1999). The dynamics of operant conditioning.
Psychological Review, 106, 20-61.
Dyal, J.A., & Sytsma, D. (1976). Relative persistence as a function
of order of reinforcement schedules. Journal of Experimental Psychology:
Animal Behavior Processes, 2, 370-375.
Ferster, C.B., & Skinner, B.F. (1957). Schedules of reinforcement.
NY: Appleton-Century-Crofts.
Flaherty, C.F. (1985). Animal learning and cognition. NY: Knopf.
Fowler, H., & Miller, N.E. (1963). Facilitation and inhibition of
runway performance by hind- and forepaw shock of various intensities. Journal
of Comparative and Physiological Psychology, 56, 801-806.
Fountain, S.B., & Husle, S.H. (1981). Extrapolation of serial stimulus
patterns by rats. Animal Learning & Behavior, 9, 381-384.
Godbout, A.C., Ziff, D.R., & Capaldi, E.J.
Gonzalez, R.C., & Bitterman, M.E. (1964). Resistance to extinction
in the rat as a function of the percentage and distribution of reinforcement.
Journal of Comparative and Physiological Psychology, 58, 258-263.
Guthrie, E.R. (1952 ). The psychology of learning. (Revised edition)
NY: Harper & Row.
Hammond, L.J. (1980). The effect of contingency upon the appetitive
conditioning of free operant behavior. Journal of the Experimental Analysis
of Behavior, 34, 297-304.
Herrnstein, R.J. (1970). On the law of effect. Journal of the Experimental
Analysis of Behavior, 13, 243-266.
Heyes, C.M., Jaldow, D., & Dawson, G.R. (1993). Observational extinction:
Observation of nonreinforced responding reduces resistance to extinction
in rats. Animal Learning & Behavior, 21, 221-225.
Hill, W.F., & Spear, N.E. (1962). Resistance to extinction as a
joint function of reward magnitude and the spacing of extinction trials.
Journal of Experimental Psychology, 64, 636-639.
Hug, J.J. (1970). Number of food pellets and the development of the
frustration effect. Psychonomic Science, 21, 59-60.
Hull, C.L. (1943). Principles of behavior. NY: Appleton-Century-Crofts.
Hull, C.L. (1952). A behavior system. New Haven: Yale.
Hulse, S.H.
Hulse, S.H. (1978). Cognitive structure and serial pattern learning
by animals. In S.H. Hulse, H. Fowler, & W.K. Honig (Eds.), Cognitive
processes in animal behavior (311-340). NJ: Erlbaum.
Hulse, S.H., & Campbell, C.E. (1975). "Thinking ahead" in rat discrimination
learning. Animal Learning & Behavior, 3, 305-311.
Hulse, S.H., Cynix, J., & Humpal, J. (1984). Cognitive processing
of pitch and rhythm structures by birds. In H.L. Roitblat, T.G. Bever,
& H.S. Terrace (Eds.), Animal cognition (183-198). NJ: Erlbaum.
Hulse, S.H., & Dorsky, N.P. (1977). Structural complexity a a determinant
of serial pattern learning. Learning and Motivation, 8, 488-506.
Hulse, S.H., & Dorsky, N.P. (1979). Serial pattern learning by rats:
Transfer of a formally defined stimulus relationship and the significance
of nonreinforcement. Animal Learning & Behavior, 7,211-220.
Kramer, T.J., & Rilling, M. (1970). Differential reinforcement of
low rates: A selective critique. Psychological Review, 74, 225-254.
Lenderhendler, I., & Baum, M. (1970). Mechanical facilitation of
the action of response prevention (flooding) in rats. Behavior Research
and Therapy, 8, 43-48.
Light, J.S., & Gantt, W.H. (1936). Essential part of reflex arc
for establishment of conditioned reflex. Formation of conditioned reflex
after exclusion of motor peripheral end. Journal of Comparative Psychology,
21, 19-36.
Mackintosh, N.J. (1974). The psychology of animal learning. CA:
Academic Press.
Maier
Mowrer, O.H., & Jones, H. (1945). Habit strength as a function of
the pattern of reinforcement. Journal of Experimental Psychology, 35,
293-311.
Nevin, J.A. (1988). Behavioral momentum and the partial reinforcement
effect. Psychological Bulletin, 103, 44-56.
Pavlik, W.B., & Carlton, P.L. (1965). A reverse partial-reinforcement
effect. Journal of Experimental Psychology, 70, 417-423.
Pavlov, I. (1927). Conditioned reflexes. London: Oxford U. Press.
Rescorla, R.A. (1997). Response-inhibition in extinction. Quarterly
Journal of Experimental Psychology. B. Comparative and Physiological Psychology,
50B, 238-252.
Roberts, W.A. (1969). Resistance to extinction following partial and
consistent reinforcement with varying magnitudes of reward. Journal
of Comparative and Physiological Psychology, 67, 395-400.
Roitblat, H.L., Bever, T.G. & Terrace, H.S. (Eds.), Animal cognition.
NJ: Erlbaum.
Scavio, M.J. (1974). Classical-classical transfer: Effects of prior
aversive conditioning upon appetitive conditioning in rabbits. Journal
of Comparative and Physiological Psychology, 86, 107-115.
Seward, J.P., & Levy, N. (1949). Sign learning as a factor in extinction.
Journal of Experimental Psychology, 39, 660-668.
Sheffield
Skinner, B.F. (1938). The behavior of organisms: An experimental
analysis. NY: Appleton-Century-Crofts
Timberlake, W. (1980). A molar equilibrium theory of learned performance.
In G.H. Bower (Ed.), The psychology of learning and motivation Vol.
14 (). NY: Academic.
Timberlake, W. , & Allison, J. (1974). Response deprivation: An
empirical approach to instrumental performance. Psychological Review,
81, 146-164.
Tulving, E. (1983). Elements of episodic memory. Oxford: Oxford
U. Press.
Wagner, A.R. (1976). Priming in STM: An information proessing mechanism
for self-generated or retrieval-generated depression in performance. In
T.J. Tighe & R.N. Leaton (Eds.), Habituation: Perspectives from
child development, animal behavior, and neurophysiology. NJ: Erlbaum.
Wagner, A.R. (1978). Expectancies and priming in STM. In S.H. Hulse,
H. Fowler, & W.K. Honig (Eds.), Cognitive processes in animal behavior
(177-209). NJ: Erlbaum.
Wagner, A.R. (1981). S.O.P.: A model of automatic memory processing
in animal behavior. In N.E. Spear & R.R. Miller (Eds.), Information
processing in animals: Memory mechanisms. NJ: Erlbaum.
Wagner, A.R.,& Brandon, S.E. (1989). Evolution of a structured connectionist
model of Pavlovian conditioning (AESOP). In S.B. Klein & R.R. Mowrer
(Eds.), Contemporary learning theories: Pavlovian conditioning and the
status of traditional learning theory (149-189). NJ: Erlbaum.
Welker, R.L., & McAuley, K. (1978). Reductions in resistance to
extinction and spontaneous recovery as a function of changes in transportational
and contextual stimuli. Animal Learning & Behavior, 6, 451-457.
1. Chapter © 1999 by Claude G. Cech
 The first two bars (the A pair) are meant to capture roughly what
happens well into extinction, at a point where the reactive inhibition
has built up dramatically. (Reactive inhibition in Figure 1 is represented
by the patterned bars: the purple bars, for those of you with a color monitor.)
In this case, the reactive inhibition has increased past the level of excitation.
Now assuming (for the sake of argument) that D and V and
K are all equal to 1, then the animal should no longer respond at
this point: Inhibition should be greater than excitation, so that there
will be a negative effective reaction potential.
The first two bars (the A pair) are meant to capture roughly what
happens well into extinction, at a point where the reactive inhibition
has built up dramatically. (Reactive inhibition in Figure 1 is represented
by the patterned bars: the purple bars, for those of you with a color monitor.)
In this case, the reactive inhibition has increased past the level of excitation.
Now assuming (for the sake of argument) that D and V and
K are all equal to 1, then the animal should no longer respond at
this point: Inhibition should be greater than excitation, so that there
will be a negative effective reaction potential.
 In any case, once the response we are interested in is emitted by
the animal, a new stimulus (the reinforcer indicated by the second
oval) enters into the context. And as you can see from this diagram, the
responses that condition to this new stimulus do not overlay the previous
response that led to it (bar pressing, for example).
In any case, once the response we are interested in is emitted by
the animal, a new stimulus (the reinforcer indicated by the second
oval) enters into the context. And as you can see from this diagram, the
responses that condition to this new stimulus do not overlay the previous
response that led to it (bar pressing, for example).
 In this figure, as the lines slope higher and higher to the left, responding
is getting faster and faster (since there will be more responses per some
interval of time). That is why I have indicated a steeper line for VR (suggesting
fastest responding in that situation). But do note the difference between
the post-RF pauses in the FR schedule (the spots where the line goes flat),
and the scallops in the FI schedule. Close inspection of real data collected
using VR schedules will also occasionally show post-RF pauses, but these
are of much smaller magnitude, and so easily missed. Normally, if you see
a schedule with noticeable pauses or staircasing, it is a good bet that
you have an FR schedule.
In this figure, as the lines slope higher and higher to the left, responding
is getting faster and faster (since there will be more responses per some
interval of time). That is why I have indicated a steeper line for VR (suggesting
fastest responding in that situation). But do note the difference between
the post-RF pauses in the FR schedule (the spots where the line goes flat),
and the scallops in the FI schedule. Close inspection of real data collected
using VR schedules will also occasionally show post-RF pauses, but these
are of much smaller magnitude, and so easily missed. Normally, if you see
a schedule with noticeable pauses or staircasing, it is a good bet that
you have an FR schedule.